题目内容
如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为 的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.
的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.
【答案】分析:采用挖填转换法:设金属片厚为h,密度为ρ.
(1)、假设剩余部分的重心还在O点不变,则必须在大圆上的对称位置再挖去一个与原来等大的小圆孔,则剩下部分的重力为G′=πR2hρg-2π•( )2hρg=
)2hρg= πR2hρg
πR2hρg
(2)、由于左边挖去了一个半径为 的小圆孔,必须在它的对应位置(左边)填上一个半径为
的小圆孔,必须在它的对应位置(左边)填上一个半径为 的小圆孔,则它的重力为G2=
的小圆孔,则它的重力为G2= πR2hρg,重心在O2上,OO2=
πR2hρg,重心在O2上,OO2= ,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将1和2综合在一起,就等效于以O′为支点的杠杆,由杠杆的平衡条件知,G2•O2O=G•OO′,求得OO′的值即可.
,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将1和2综合在一起,就等效于以O′为支点的杠杆,由杠杆的平衡条件知,G2•O2O=G•OO′,求得OO′的值即可.
解答:解:(采用挖填转换法)
①假设剩余部分的重心还在O点不变,则必须在大圆上的对称位置再挖去一个与原来等大的小圆孔.
则剩下部分的重力为G′=πR2hρg-2π•( )2hρg=
)2hρg= πR2hρg
πR2hρg
如答图甲(设金属片厚为h,密度为p).
②由于左边挖去了一个半径为 的小圆孔,必须在它的对应位置(左边)填上一个半径为
的小圆孔,必须在它的对应位置(左边)填上一个半径为 的小圆孔,
的小圆孔,
则它的重力为G2=π•( )2hρg=
)2hρg= πR2hρg,重心在O2上,且OO2=
πR2hρg,重心在O2上,且OO2= ,如图乙,
,如图乙,
设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将①和②综合在一起,就等效于以O′为支点的杠杆.
如图丙,由杠杆的平衡条件得G2•O2O=G•OO′,即 πR2hρg•(
πR2hρg•( -OO′)=
-OO′)= πR2hρg•OO′,解得OO′=
πR2hρg•OO′,解得OO′= .
.

点评:本题利用了采用挖填转换法,涉及到物理中的密度知识,杠杆平衡条件的知识,是一道跨学科的题.
(1)、假设剩余部分的重心还在O点不变,则必须在大圆上的对称位置再挖去一个与原来等大的小圆孔,则剩下部分的重力为G′=πR2hρg-2π•(
 )2hρg=
)2hρg= πR2hρg
πR2hρg(2)、由于左边挖去了一个半径为
 的小圆孔,必须在它的对应位置(左边)填上一个半径为
的小圆孔,必须在它的对应位置(左边)填上一个半径为 的小圆孔,则它的重力为G2=
的小圆孔,则它的重力为G2= πR2hρg,重心在O2上,OO2=
πR2hρg,重心在O2上,OO2= ,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将1和2综合在一起,就等效于以O′为支点的杠杆,由杠杆的平衡条件知,G2•O2O=G•OO′,求得OO′的值即可.
,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将1和2综合在一起,就等效于以O′为支点的杠杆,由杠杆的平衡条件知,G2•O2O=G•OO′,求得OO′的值即可.解答:解:(采用挖填转换法)
①假设剩余部分的重心还在O点不变,则必须在大圆上的对称位置再挖去一个与原来等大的小圆孔.
则剩下部分的重力为G′=πR2hρg-2π•(
 )2hρg=
)2hρg= πR2hρg
πR2hρg如答图甲(设金属片厚为h,密度为p).
②由于左边挖去了一个半径为
 的小圆孔,必须在它的对应位置(左边)填上一个半径为
的小圆孔,必须在它的对应位置(左边)填上一个半径为 的小圆孔,
的小圆孔,则它的重力为G2=π•(
 )2hρg=
)2hρg= πR2hρg,重心在O2上,且OO2=
πR2hρg,重心在O2上,且OO2= ,如图乙,
,如图乙,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将①和②综合在一起,就等效于以O′为支点的杠杆.
如图丙,由杠杆的平衡条件得G2•O2O=G•OO′,即
 πR2hρg•(
πR2hρg•( -OO′)=
-OO′)= πR2hρg•OO′,解得OO′=
πR2hρg•OO′,解得OO′= .
.
点评:本题利用了采用挖填转换法,涉及到物理中的密度知识,杠杆平衡条件的知识,是一道跨学科的题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为
如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为 如图所示,在一个大圆形区域内包含一个小圆的区域,大圆的半径为2,小圆的半径为1,一个飞镖落在阴影部分的概率是
如图所示,在一个大圆形区域内包含一个小圆的区域,大圆的半径为2,小圆的半径为1,一个飞镖落在阴影部分的概率是 如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为
如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为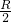 的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.
的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置. 如图所示,在一个大圆形区域内包含一个小圆的区域,大圆的半径为2,小圆的半径为1,一个飞镖落在阴影部分的概率是________.
如图所示,在一个大圆形区域内包含一个小圆的区域,大圆的半径为2,小圆的半径为1,一个飞镖落在阴影部分的概率是________.