Question

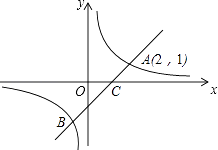
【题目】如图，反比例函数y= （k≠0）的图象经过A，B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE的面积为2，则k的值为 ．

Answer 1

【答案】-
【解析】解：设点B坐标为（a，b），则DO=﹣a，BD=b
∵AC⊥x轴，BD⊥x轴
∴BD∥AC
∵OC=CD
∴CE= BD= b，CD= DO= a
∵四边形BDCE的面积为2
∴ （BD+CE）×CD=2，即 （b+ b）×（﹣ a）=2
∴ab=﹣
将B（a，b）代入反比例函数y= （k≠0），得
k=ab=﹣
所以答案是：﹣

【考点精析】利用比例系数k的几何意义和平行线分线段成比例对题目进行判断即可得到答案，需要熟知几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积；三条平行线截两条直线，所得的对应线段成比例．