题目内容
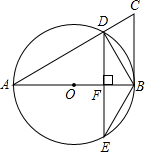
 已知,如图,BC是以线段AB为直径的⊙O的切线,AC交⊙O于点D,过点D作弦DE⊥AB,垂足为点F,连接BD、BE..
已知,如图,BC是以线段AB为直径的⊙O的切线,AC交⊙O于点D,过点D作弦DE⊥AB,垂足为点F,连接BD、BE..
(1)仔细观察图形并写出四个不同类型的正确结论:①______,②______,
③______,④______(不添加其它字母和辅助线,不必证明);
(2)若∠A=30°,⊙O的半径为2,求△BDE的面积.
解:(1)①AD⊥BD,(BC⊥AB),(∠ADB=∠ABC=90°);②DE∥BC;③∠BDE=∠E=∠A=∠CBD;④BD=BE,DF=EF,⑤△BFD≌△BFE;⑥ =
= ,
, =
= ,⑦S△DBF=S△EBF 等.
,⑦S△DBF=S△EBF 等.
故答案为:①AD⊥BD,②DE∥BC,③BD=BE,④ =
= ;
;
(2)∵AB是直径,
∴∠ADB=90°,
∵⊙O的半径为2,
∴AB=4,
∵∠A=30°,
∴
 ,
,
∵AB⊥DE,
DF=EF= DE,
DE,
在Rt△ADF中,∠A=30°,
∴

 ,BF=AB-AF=4-3=1,
,BF=AB-AF=4-3=1,
∴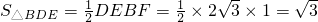 .
.
分析:(1)由BC是以线段AB为直径的⊙O的切线,可得AD⊥BD,AB⊥BC,继而由DE⊥AB,可得DE∥BC,由垂径定理,易得BD=BE, =
= 等;
等;
(2)由AB为直径,∠A=30°,⊙O的半径为2,根据直角三角形的性质,易求得BD的长,继而由垂径定理与勾股定理即可求得答案.
点评:此题考查了切线的性质、垂径定理、圆周角定理以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.
 =
= ,
, =
= ,⑦S△DBF=S△EBF 等.
,⑦S△DBF=S△EBF 等.故答案为:①AD⊥BD,②DE∥BC,③BD=BE,④
 =
= ;
;(2)∵AB是直径,
∴∠ADB=90°,
∵⊙O的半径为2,
∴AB=4,
∵∠A=30°,
∴

 ,
,∵AB⊥DE,
DF=EF=
 DE,
DE,在Rt△ADF中,∠A=30°,
∴


 ,BF=AB-AF=4-3=1,
,BF=AB-AF=4-3=1,∴
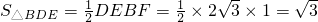 .
.分析:(1)由BC是以线段AB为直径的⊙O的切线,可得AD⊥BD,AB⊥BC,继而由DE⊥AB,可得DE∥BC,由垂径定理,易得BD=BE,
 =
= 等;
等;(2)由AB为直径,∠A=30°,⊙O的半径为2,根据直角三角形的性质,易求得BD的长,继而由垂径定理与勾股定理即可求得答案.
点评:此题考查了切线的性质、垂径定理、圆周角定理以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 F,连接BD、BE.
F,连接BD、BE. F,连接BD、BE.
F,连接BD、BE. ,求⊙O的半径r.
,求⊙O的半径r. ,求⊙O的半径r.
,求⊙O的半径r.
 ,求⊙O的半径r.
,求⊙O的半径r.
 ,求⊙O的半径r.
,求⊙O的半径r.