题目内容
 已知如图⊙O的半径为3,过⊙O外的一点B作⊙O的切线BM,M为切点,BO交⊙O于A,过A点作BO的垂线,交BM于P点,BO=5,求:MP的长.
已知如图⊙O的半径为3,过⊙O外的一点B作⊙O的切线BM,M为切点,BO交⊙O于A,过A点作BO的垂线,交BM于P点,BO=5,求:MP的长.分析:连接OM,根据切线的性质得到直角三角形,根据勾股定理求得BM的长.再根据切线长定理和勾股定理列方程求得MP的长.
解答:解:连接OM,则OM⊥BM,
在Rt△BOM中,OM=3,BO=5,
根据勾股定理,得BM=4;
∵AP⊥OB,
∴AP是圆的切线,
又PM是圆的切线,
∴AP=MP;
在Rt△APB中,
设AP=x,AB=5-3=2,BP=4-x;
根据勾股定理得:
(4-x)2=x2+4
x=
,
∴MP=
.
在Rt△BOM中,OM=3,BO=5,
根据勾股定理,得BM=4;

∵AP⊥OB,
∴AP是圆的切线,
又PM是圆的切线,
∴AP=MP;
在Rt△APB中,
设AP=x,AB=5-3=2,BP=4-x;
根据勾股定理得:
(4-x)2=x2+4
x=
| 3 |
| 2 |
∴MP=
| 3 |
| 2 |
点评:本题考查了勾股定理和切线的判定、切线的性质以及切线长的定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


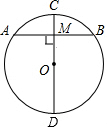 已知:如图⊙O的半径为5,CD为直径,AB为弦,CD⊥AB于M,若AB=6,求DM的长.
已知:如图⊙O的半径为5,CD为直径,AB为弦,CD⊥AB于M,若AB=6,求DM的长.
 已知如图⊙O的半径为3,过⊙O外的一点B作⊙O的切线BM,M为切点,BO交⊙O于A,过A点作BO的垂线,交BM于P点,BO=5,求:MP的长.
已知如图⊙O的半径为3,过⊙O外的一点B作⊙O的切线BM,M为切点,BO交⊙O于A,过A点作BO的垂线,交BM于P点,BO=5,求:MP的长.