题目内容
20．已知△ABC的两边长分别是6和10，设第三边上的中线长为m，则m的取值范围是2＜m＜8．分析 作出草图，延长AD到E，使DE=AD，连接CE，利用“边角边”证明△ABD和△ECD全等，然后根据全等三角形对应边相等可得CE=AB，再根据三角形的任意两边之和大于第三边，两边之和小于第三边求出AE的取值范围，便不难得出m的取值范围．
解答 解：如图，延长AD到E，使DE=AD，连接CE，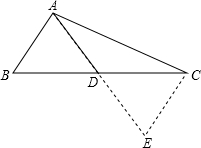
∵AD是△ABC的中线，
∴BD=CD，
在△ABD和△ECD中，
$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$，
∴△ABD≌△ECD（SAS），
∴CE=AB，
∵AB=6，AC=10，
∴10-6＜AE＜10+6，
即4＜AE＜16，
∴2＜m＜8．
故答案为：2＜m＜8．
点评 本题考查了全等三角形的判定与性质，三角形的三边关系，“遇中线加倍延”通过作辅助线构造出全等三角形是解题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
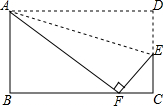如图，小红将长方形ABCD沿AE折叠，顶点D恰好落在BC边上的F处，已知AB=8，BC=10，试求折痕AE的长．
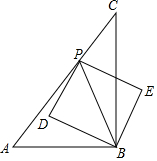定义，若以一条线段为对角线作正方形，则称该正方形为这条线段的“对角线正方形”，如图，在△ABC中，∠ABC=90°，AB=3cm，BC=4cm，点P从点C出发，沿折线CA-AB以5cm/s的速度运动，当电P与点B不重合时，作线段PB的“对角线正方形”，设点P的运动时间为t（s），线段PB的“对角线正方形”的面积为S（cm2）．