题目内容
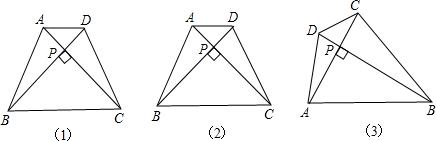
 已知:等腰梯形ABCD,AD∥BC,对角线AC⊥BD,相交于点O,AD=3cm,BC=7cm,求梯形的面积S.
已知:等腰梯形ABCD,AD∥BC,对角线AC⊥BD,相交于点O,AD=3cm,BC=7cm,求梯形的面积S.
分析:做OE⊥AD并反向延长OE交BC于点F,由等腰梯形为轴对称图形可知OA=OD,OB=OC,已知AC⊥BD,可证△AOD,△BOC为等腰直角三角形,故有OE=
AD=
,OF=
BC=
,从而可求EF的长,即等腰梯形的高,再计算梯形的面积.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
解答: 解:做OE⊥AD并反向延长OE交BC于点F,
解:做OE⊥AD并反向延长OE交BC于点F,
∵四边形ABCD是等腰梯形,
∴点O在梯形ABCD的对称轴上,
∴OA=OD,OB=OC,
设对称轴与AD、BC分别交于E、F,
则OE=
AD=
,OF=
BC=
,
∴EF=OE+OF=5,
∴S梯形=
(AD+BC)•EF=
×(3+7)×5=25.
 解:做OE⊥AD并反向延长OE交BC于点F,
解:做OE⊥AD并反向延长OE交BC于点F,∵四边形ABCD是等腰梯形,
∴点O在梯形ABCD的对称轴上,
∴OA=OD,OB=OC,
设对称轴与AD、BC分别交于E、F,
则OE=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴EF=OE+OF=5,
∴S梯形=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等腰梯形的轴对称性,根据轴对称性和对角线互相垂直证明△AOD,△BOC为等腰直角三角形是解题的关键,本题还可以平移一条对角线,将梯形面积转化为三角形面积求解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 △EBF,点A落在点E处,点C落在点F处,连接CF.请你画出图形,并按下面要求完成本题.
△EBF,点A落在点E处,点C落在点F处,连接CF.请你画出图形,并按下面要求完成本题. 如图,已知在等腰梯形ABCD中,AD∥BC,∠ABC=45°,两腰的和为8cm,点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,则EF的长为
如图,已知在等腰梯形ABCD中,AD∥BC,∠ABC=45°,两腰的和为8cm,点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,则EF的长为 cm
cm