题目内容
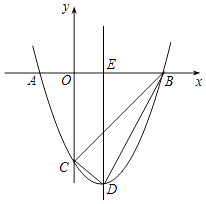
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(a,0)(其中a>0),作AB∥y轴交反比例函数![]() (k>0,x>0)的图象于点B.
(k>0,x>0)的图象于点B.
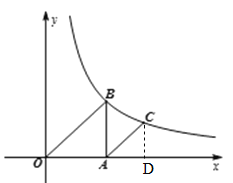
(1)当△OAB的面积为2时,①求k的值;②若a=2,过A点作AC∥OB交![]() (k>0,x>0)图象于点C,求C的横坐标;
(k>0,x>0)图象于点C,求C的横坐标;
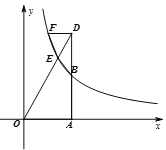
(2)若D为射线AB上一点,连接OD交反比例函数图象于点E,DF∥x轴交反比例函数![]() (k>0,x>0)的图象于点F,连接EF、EB,试猜想:
(k>0,x>0)的图象于点F,连接EF、EB,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
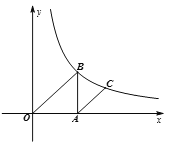
【答案】(1)①4;②点C横坐标为![]() ;(2) 不变,比值为1.
;(2) 不变,比值为1.
【解析】(1)①由B(a,![]() ),得到OA=a,AB=
),得到OA=a,AB=![]() , 由S△OAB=
, 由S△OAB=![]() ·AB·OA=2,即可得到结论;
·AB·OA=2,即可得到结论;
②过点C作CD⊥AO于点D,得到B(2,2),设AD=b,则C(2+b,![]() ),可证△OAB∽△ADC,得到
),可证△OAB∽△ADC,得到![]() ,即
,即![]() ,解方程得到b的值,从而得到点C的横坐标.
,解方程得到b的值,从而得到点C的横坐标.
(2)不变,比值为1.设![]() ,则yOE=
,则yOE=![]() ,由S△DBE=
,由S△DBE=![]()
![]() ,S△DEF=
,S△DEF=![]() ,代入
,代入![]()
![]() 化简即可得到结论.
化简即可得到结论.
(1)①∵B(a,![]() ),∴OA=a,AB=
),∴OA=a,AB=![]() , ∴S△OAB=
, ∴S△OAB=![]() ·AB·OA=2,∴k=4;
·AB·OA=2,∴k=4;
②过点C作CD⊥AO于点D.
∵a=2,∴B(2,2),
设AD=b,∴C(2+b,![]() ).
).
∵AC∥OB,∴∠BOA=∠CAD.
∵∠BAO=∠CDA,∴△OAB∽△ADC,
∴![]() ,∴
,∴![]() ,∴b=
,∴b=![]() ,解得:b=-1+
,解得:b=-1+![]() (负值舍去),∴点C的横坐标=2-1+
(负值舍去),∴点C的横坐标=2-1+![]() =
=![]() .
.
(2)不变,比值为1.理由如下:
设![]() yOE=
yOE=![]() ∴
∴![]() .
.
∵S△DBE=![]()
![]() ,S△DEF=
,S△DEF=![]()
∴![]() =
=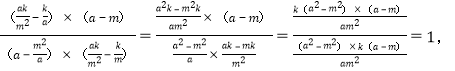 ∴
∴![]() =1.
=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目