Question

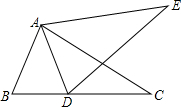已知：如图，点D为△ABC的边BC上一点，且AB=AD，点E为△ABC外一点，连接AE、DE，使得∠ADE=∠B，∠CAE=∠BAD．
求证：BC=DE．

Answer 1

分析：首先证明∠1=∠3，再加上条件∠ADE=∠B，AB=AD可利用ASA定理证明△ABC≌△ADE，再根据全等三角形对应边相等可得结论BC=DE．

解答：证明：∵∠CAE=∠BAD，
∴∠CAE+∠2=∠BAD+∠2，
即∠1=∠3，
在△ABC和△ADE中

∠1=∠3 AB=AD ∠B=∠ADE

，
∴△ABC≌△ADE（ASA），
∴BC=DE．

点评：本题考查三角形全等的判定方法与性质，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL，
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．