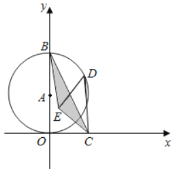
题目内容
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 相交于点
相交于点![]() ,
,![]() .
.
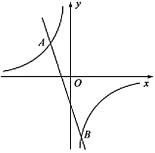
(1)求出直线![]() 的表达式;
的表达式;
(2)在![]() 轴上有一点
轴上有一点![]() 使得
使得![]() 的面积为18,求出点
的面积为18,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当点
;(2)当点![]() 在原点右侧时,
在原点右侧时,![]() ,当点
,当点![]() 在原点左侧时,
在原点左侧时,![]() .
.
【解析】
(1)通过点A的坐标确定反比例函数的解析式,再求得B的坐标,利用待定系数法将A,B的坐标代入,即可得到一次函数的解析式;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,得到
,得到![]() ,即
,即![]() ,分情况讨论即可解决.
,分情况讨论即可解决.
解:(1)∵![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,![]() ,
,
又点![]() 在
在![]() 的图象上,
的图象上,![]() ,即
,即![]() .
.
将点![]() ,
,![]() 的坐标代入
的坐标代入![]() ,得
,得![]() ,
,
解得![]() .
.
∴直线的表达式为![]() .
.
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
当![]() 时,解得
时,解得![]() .即
.即![]() .
.
分别过点![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .
.
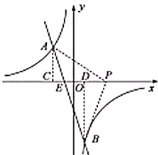
![]() .
.
又![]() ,即
,即![]() ,∴
,∴![]() .
.
当点![]() 在原点右侧时,
在原点右侧时,![]() ,
,
当点![]() 在原点左侧时,
在原点左侧时,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目