题目内容
如图，直线
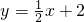交x轴于A，交y轴于B，交双曲线
于C，A、D关于y轴对称，若S四OBCD=6，则k=________．
2.5
分析：过C作CE⊥x轴于E，求出A、B的坐标，求出D的坐标，求出AD，设C的坐标是（x，
x+2），根据面积得出×8×（x+2）-×|-4|×2=6，求出x，得出C的坐标，代入双曲线的解析式求出即可．
解答：过C作CE⊥x轴于E，
∵y=x+2，
∴当x=0时，y=2；当y=0时，x=-4；
即A的坐标是（-4，0），B（0，2），
∵A、D关于y轴对称，
∴D的坐标是（4，0），
即AD=4-（-4）=8，
∵C在直线y=x+2上，
∴设C的坐标是（x，x+2），
∵S四OBCD=6，
∴×8×（x+2）-×|-4|×2=6，
解得：x=1，
x+2=2.5，
即C的坐标是（1，2.5），
代入y=
得：k=2.5，
故答案为：2.5．
点评：本题考查了一次函数与反比例函数的交点，用待定系数法求反比例函数的解析式，三角形的面积等知识点的应用，关键是求出C的坐标，题目综合性比较强，但题目比较典型．
分析：过C作CE⊥x轴于E，求出A、B的坐标，求出D的坐标，求出AD，设C的坐标是（x，
x+2），根据面积得出×8×（x+2）-×|-4|×2=6，求出x，得出C的坐标，代入双曲线的解析式求出即可．解答：过C作CE⊥x轴于E，
∵y=
x+2，∴当x=0时，y=2；当y=0时，x=-4；
即A的坐标是（-4，0），B（0，2），
∵A、D关于y轴对称，
∴D的坐标是（4，0），
即AD=4-（-4）=8，
∵C在直线y=
x+2上，∴设C的坐标是（x，
x+2），∵S四OBCD=6，
∴
×8×（x+2）-×|-4|×2=6，解得：x=1，
x+2=2.5，即C的坐标是（1，2.5），
代入y=
得：k=2.5，故答案为：2.5．
点评：本题考查了一次函数与反比例函数的交点，用待定系数法求反比例函数的解析式，三角形的面积等知识点的应用，关键是求出C的坐标，题目综合性比较强，但题目比较典型．
练习册系列答案
小学能力测试卷系列答案
相关题目
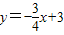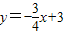交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．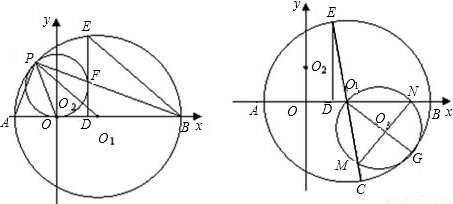
交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．
交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．
交x轴于点A，交直线
于点B（2，m）．矩形CDEF的边DC在x轴上，D在C的左侧，EF在x轴的上方，DC=2，DE=4．当点C的坐标为（-2，0）时，矩形CDEF开始以每秒2个单位的速度沿x轴向右运动，运动时间为t秒．
交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．