��Ŀ����
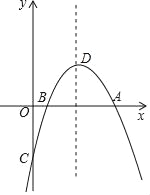
����Ŀ����ͼ��������y��ax2+2ax+c��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�AB��4����y�ύ�ڵ�C��OC��OA����DΪ�����ߵĶ��㣮
��1���������ߵĽ���ʽ��
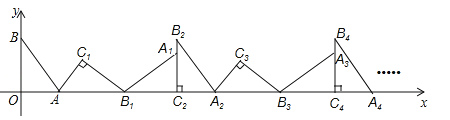
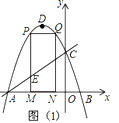
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ1����P�ڵ�Q��ߣ�������PQNM���ܳ����ʱ����m��ֵ���������ʱ����AEM�������
��3����(2)��������,������PMNQ���ܳ����ʱ,����DQ,����������һ��F��y���ƽ����,��ֱ��AC���ڵ�G(��G�ڵ�F���Ϸ�),��FG=![]() DQ,���F������.
DQ,���F������.
���𰸡���1��y=-x2-2x+3����2��m=-2����AEM�����Ϊ![]() ����3��F��-4��-5����1��0����
����3��F��-4��-5����1��0����
��������
��1������������y=ax2+2ax+c���ɵ�C��0��c�����Գ���Ϊx=-1���ٸ���OC=OA��AB=4���ɵ�A��-3��0����������������y=ax2+2ax+3���������ߵĽ���ʽΪy=-x2-2x+3��
��2�����ݵ�M��m��0�����ɵþ���PQNM�У�P��m��-m2-2m+3����Q��-2-m��-m2-2m+3�����ٸ��ݾ���PQNM���ܳ�=2��PM+PQ��=-2��m+2��2+10���ɵõ�m=-2ʱ������PQNM���ܳ������ֵ10��M������Ϊ��-2��0���������ֱ��ACΪy=x+3��AM=1�����E��-2��1����ME=1���ݴ������AEM�������
��3���ڣ�2���Ļ����ϣ��жϳ�NӦ��ԭ���غϣ�Q����C���غϣ����DQ=DC=![]() ���ٽ������̣�n+3��-��-n2-2n+3��=4���ɣ�
���ٽ������̣�n+3��-��-n2-2n+3��=4���ɣ�
�⣺��1����������y=ax2+2ax+c���ɵ�C��0��c�����Գ���Ϊx=![]() =-1��
=-1��
��OC=OA��
��A��-c��0����B��-2+c��0����
��AB=4��
��-2+c-��-c��=4��
��c=3��
��A��-3��0����
����������y=ax2+2ax+3����
0=9a-6a+3��
���a=-1��
�������ߵĽ���ʽΪy=-x2-2x+3��
��2����ͼ1����M��m��0����PM��x�ᣬ

��P��m��-m2-2m+3����
�֡߶Գ���Ϊx=-1��PQ��AB��
��Q��-2-m��-m2-2m+3����
�֡�QN��x�ᣬ
�����PQNM���ܳ�
=2��PM+PQ��
=2[��-m2-2m+3��+��-2-m-m��]
=2��-m2-4m+1��
=-2��m+2��2+10��
�൱m=-2ʱ������PQNM���ܳ������ֵ10��
��ʱ��M��-2��0����
��A��-3��0����C��0��3�����ɵ�
ֱ��ACΪy=x+3��AM=1��
�൱x=-2ʱ��y=1����E��-2��1����ME=1��
���AEM�����= ![]() ��
��
��3����M��-2��0���������ߵĶԳ���Ϊx=-l��
��NӦ��ԭ���غϣ�Q����C���غϣ�
��DQ=DC��
��x=-1����y=-x2-2x+3�����y=4��
��D��-1��4����
��DQ=DC=![]() ��
��
��FG=2![]() DQ��
DQ��
��FG=4��
��F��n��-n2-2n+3������G��n��n+3����
�ߵ�G�ڵ�F���Ϸ���FG=4��
�ࣨn+3��-��-n2-2n+3��=4��
���n=-4��n=1��
��F��-4��-5����1��0����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�