题目内容
如图,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
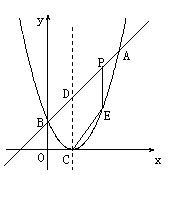 |
(1) ∵ 点A(3,4)在直线y=x+m上,∴ 4=3+m. ∴ m=1.
设所求二次函数的关系式为y=a(x-1)2.
∵ 点A(3,4)在二次函数y=a(x-1)2的图象上, ∴ 4=a(3-1)2, ∴ a=1.
∴ 所求二次函数的关系式为y=(x-1)2. 即y=x2-2x+1.
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE =(x+1)-(x2-2x+1) =-x2+3x. 即h=-x2+3x (0<x<3).
(3) 存在.
解法1:要使四边形DCEP是平行四边形,必需有PE=DC.
∵ 点D在直线y=x+1上,∴ 点D的坐标为(1,2),∴ -x2+3x=2 .
即x2-3x+2=0 .解之,得 x1=2,x2=1 (不合题意,舍去)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.
解法2:要使四边形DCEP是平行四边形,必需有BP∥CE.
设直线CE的函数关系式为y=x+b.∵ 直线CE 经过点C(1,0),
∴ 0=1+b,∴ b=-1 .∴ 直线CE的函数关系式为y=x-1 .
∴ ![]() 得x2-3x+2=0.
得x2-3x+2=0.
解之,得 x1=2,x2=1 (不合题意,舍去)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.

 备战中考寒假系列答案
备战中考寒假系列答案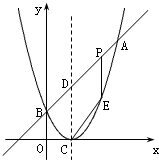 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.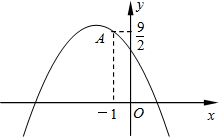 (2012•高淳县一模)如图,已知二次函数y=-
(2012•高淳县一模)如图,已知二次函数y=-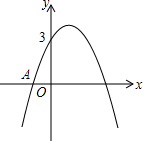 (2013•江宁区二模)如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
(2013•江宁区二模)如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
 如图,已知二次函数y=(x-1)2的图象的顶点为C点,图象与直线y=x+m的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
如图,已知二次函数y=(x-1)2的图象的顶点为C点,图象与直线y=x+m的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.