题目内容
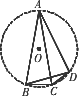
如图,D是△ABC外的一点,且∠ABD=∠ACD=60°,∠ADB=90°-![]() ∠BDC,求证:AB=AC.
∠BDC,求证:AB=AC.
答案:
解析:
解析:
|
分析:作△ABD的外接圆⊙O,由∠ABD=∠ACD可知,点C也在⊙O上,可以把证明AB=AC转化为证明 证明:作△ABD的外接圆⊙O. 因为∠ABD=∠ACD,所以点C也在⊙O上. 因为∠ACD=60°,所以∠CAD+∠ADC=120°. 所以∠CBD=∠CAD=120°-∠ADC =120°-(∠ADB+∠BDC) =120°-90°- =30°- 因为∠ABC=∠ABD+∠CBD=90°- 所以∠ADB=∠ABC.所以 所以AB=AC. 点评:在证明线段相等时,可以转化为证明弧相等,由此想到添加外接圆. |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图,BE是△ABC的外接⊙O的直径,CD是△ABC的高.
如图,BE是△ABC的外接⊙O的直径,CD是△ABC的高.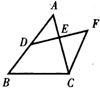

 如图,⊙O是△ABC的
如图,⊙O是△ABC的