Question

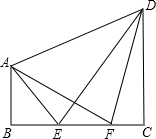如图，在直角梯形ABCD中，∠B=∠C=9O°，E、F是BC上两点，若AD=ED，∠ADE=30°，∠FDC=15°，则下列结论：①∠AED=∠DFC；②BE=2CF；③AB-CF=EF；④S_△DAF：S_△DEF=AF：EF．其中正确的结论是

1. A.
   ①③
2. B.
   ②④
3. C.
   ①③④
4. D.
   ①②④

Answer 1

C
分析：①由AD=DE，∠ADE=30°，可求∠AED的度数，已知∠FDC=15°，利用互余关系可求∠DFC的度数，证明结论；
②其中用到了AF=2AB，即角AFB=30度，这个条件由四点共圆之后的角AFB=角ADE=30度得到
结论②是错误的，因为AF＞BF，即2AB＞BE+EF，把结论③中EF=2AB-2CF代入得到2CF＞BE，
③作E、F关于直线CD的对称点E'，F'，则可以证明三角形DAF全等于三角形DE'F，所以E'F=2CF+EF=AF=2AB，所以AB-CF=1/2EF．结论④是正确的，根据三角形DAF全等于三角形DE'F，则可得：S_△DAF：S_△DEF=AF：EF．
解答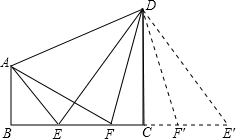：解：
①∵∠DFC=∠DAE=75°，
∴AEFD四点共圆，
则所以∠AFB=∠ADE=30°，
所以证明∠AED=∠DFC
故①正确；
②其中用到了AF=2AB，即角AFB=30度，这个条件由四点共圆之后的角AFB=角ADE=30度得到
结论②是错误的，因为AF＞BF，即2AB＞BE+EF，把结论③中EF=2AB-2CF代入得到2CF＞BE，
故②错误；
③作E、F关于直线CD的对称点E'，F'，则可以证明三角形DAF全等于三角形DE'F，所以E'F=2CF+EF=AF=2AB，所以AB-CF=EF，结论③正确
结论④是正确的，根据三角形DAF全等于三角形DE'F，则可得：S_△DAF：S_△DEF=AF：EF
故④正确．
点评：本题考查了直角梯形，题主要考查了梯形的性质，矩形的判定，相似三角形的判定和性质以及一次函数的综合应用，核心是三角形DAF全等于三角形DE'F，一个很重的环节，认真思考解决它就迎刃而解．