题目内容
已知a,b,c为互不相同的有理数,满足 =(a+
=(a+ )(c+
)(c+ ),则符合条件的a,b,c的组数共有
),则符合条件的a,b,c的组数共有
- A.0组
- B.1组
- C.2组
- D.4组
A
分析:首先整理 =(a+
=(a+ )(c+
)(c+ ),得出b2+2
),得出b2+2 b=ac+(a+c)
b=ac+(a+c) ,再分析得出无理数的系数部分相等,有理数部分也相等,进而求出.
,再分析得出无理数的系数部分相等,有理数部分也相等,进而求出.
解答:∵(b+ )2=(a+
)2=(a+ )(c+
)(c+ ),∴b2+2
),∴b2+2 b=ac+(a+c)
b=ac+(a+c) ,因为a b c为有理数所以无理数的系数部分相等,有理数部分也相等,即b2=ac①,2b=a+c②,将②代入①得:(a-c)2=0,得a=c,与a b c为互不相同的有理数矛盾,所以符合条件的a b c共有0组.
,因为a b c为有理数所以无理数的系数部分相等,有理数部分也相等,即b2=ac①,2b=a+c②,将②代入①得:(a-c)2=0,得a=c,与a b c为互不相同的有理数矛盾,所以符合条件的a b c共有0组.
故选:A.
点评:此题主要考查了二次根式的综合应用,去掉括号后由已知可得出无理数的系数部分相等,有理数部分也相等,这是解决问题的关键.
分析:首先整理
 =(a+
=(a+ )(c+
)(c+ ),得出b2+2
),得出b2+2 b=ac+(a+c)
b=ac+(a+c) ,再分析得出无理数的系数部分相等,有理数部分也相等,进而求出.
,再分析得出无理数的系数部分相等,有理数部分也相等,进而求出.解答:∵(b+
 )2=(a+
)2=(a+ )(c+
)(c+ ),∴b2+2
),∴b2+2 b=ac+(a+c)
b=ac+(a+c) ,因为a b c为有理数所以无理数的系数部分相等,有理数部分也相等,即b2=ac①,2b=a+c②,将②代入①得:(a-c)2=0,得a=c,与a b c为互不相同的有理数矛盾,所以符合条件的a b c共有0组.
,因为a b c为有理数所以无理数的系数部分相等,有理数部分也相等,即b2=ac①,2b=a+c②,将②代入①得:(a-c)2=0,得a=c,与a b c为互不相同的有理数矛盾,所以符合条件的a b c共有0组.故选:A.
点评:此题主要考查了二次根式的综合应用,去掉括号后由已知可得出无理数的系数部分相等,有理数部分也相等,这是解决问题的关键.

练习册系列答案
相关题目
已知a,b,c是互不相等的正实数,且
=
=
,则代数式
的值为( )
| a-b |
| x |
| b-c |
| y |
| c-a |
| z |
| 2011x+2011y+2011z |
| 2009a+2010b+2011c |
| A、2009 | B、2010 |
| C、2011 | D、0 |
已知a、b、c是互不相等的实数,且
=
=
,则x+y+z的值为( )
| x |
| a-b |
| y |
| b-c |
| z |
| c-a |
| A、-1 | B、0 | C、1 | D、2 |
已知a,b,c为互不相同的有理数,满足(b+
)2=(a+
)(c+
),则符合条件的a,b,c的组数共有( )
| 2 |
| 2 |
| 2 |
| A、0组 | B、1组 | C、2组 | D、4组 |
已知a,b,c是互不相等的正实数,且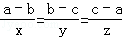 ,则代数式
,则代数式 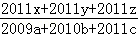 的值为( )
的值为( )
| A.2009 | B.2010 | C.2011 | D.0 |