Question

 

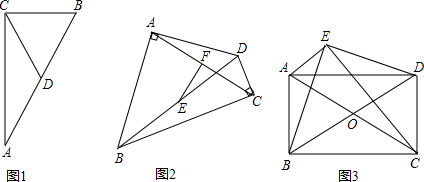
1.如图1，在矩形ABCD中，AB=2BC，M是AB的中点．直接写出∠BMD与∠ADM的倍数关系；

2.如图2，若四边形ABCD是平行四边形， AB=2BC，M是AB的中点，过C作CE⊥AD与AD所在直线交于点E．

①若∠A为锐角，则∠BME与∠AEM有怎样的倍数关系，并证明你的结论；

②当时，上述结论成立；

当 时，上述结论不成立．

 

Answer 1

 

1.∠BMD= 3 ∠ADM

2.见解析有。

当0°<∠A<120°时，结论成立；

当时，结论不成立.

解析:（1）∠BMD= 3 ∠ADM                          ………… 2分

（2）联结CM，取CE的中点F，联结MF，交DC于N

∵M是AB的中点，∴MF∥AE∥BC，

∴∠AEM=∠1，∠2=∠4，    ……… 3分

∵AB=2BC，∴BM=BC，∴∠3=∠4.            

     ∵CE⊥AE，∴MF⊥EC，又∵F是EC的中点，

∴ME=MC，∴∠1=∠2.    ……….4分

∴∠1=∠2=∠3.

∴∠BME =3∠AEM.        ………. 5分

（3）当0°<∠A<120°时，结论成立；

当时，结论不成立.