题目内容
在RT△ACB中，∠ACB=90°，AC=6，BC=8，P、Q两点分别是边AC、BC上的动点，将△PCQ沿PQ翻折，C点的对应点为C′，连接AC′，则AC′的最小值是________．
2
分析：当P与B重合，折叠后C的对称点在AB上时，AC′最小，根据对称性即可求解．
解答：∵RT△ACB中，∠ACB=90°，AC=6，BC=8．
∴AB=
=10，
当P与B重合，折叠后C的对称点在AB上时，AC′最小．
∴BC′=BC=8，
∴AC′=10-8=2．
故答案是：2．
点评：本题主要考查了图形的折叠，正确确定P的位置是解题的关键．
分析：当P与B重合，折叠后C的对称点在AB上时，AC′最小，根据对称性即可求解．
解答：∵RT△ACB中，∠ACB=90°，AC=6，BC=8．
∴AB=
=10，当P与B重合，折叠后C的对称点在AB上时，AC′最小．
∴BC′=BC=8，
∴AC′=10-8=2．
故答案是：2．
点评：本题主要考查了图形的折叠，正确确定P的位置是解题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
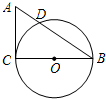在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D．
（2013•湖州）如图，已知在Rt△ACB中，∠C=90°，AB=13，AC=12，则cosB的值为
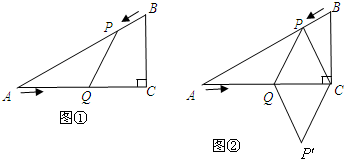
（2013•丹东一模）在Rt△ACB中，∠C=90°，AC=BC，一直角三角板的直角顶角O在AB边的中点上，这块三角板绕O点旋转，两条直角边始终与AC、BC边分别相交于E、F，连接EF，则在运动过程中，△OEF与△ABC的关系是（ ）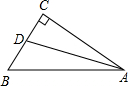
如图所示，在Rt△ACB中，∠C=90°，AD平分∠BAC，若BC=16，BD=10，则点D到AB的距离是（ ）