题目内容
(本题满分7分)已知代数式A=2x2+3xy+2y-1,B=x2-xy+x-
(1)当x=y=-2时,求A-2B的值;
(2)若A-2B的值与x的取值无关,求y的值.
(1)20;(2)=
【解析】
试题分析:(1)把A=2x2+3xy+2y-1,B=x2-xy+x- 代入A-2B合并同类项,化为最简的多项式,再x=y=-2,代入求值即可;(2)A-2B合并同类项,化为最简的多项式,其的值与x的取值无关,所以令x的系数为0,求y的值.
代入A-2B合并同类项,化为最简的多项式,再x=y=-2,代入求值即可;(2)A-2B合并同类项,化为最简的多项式,其的值与x的取值无关,所以令x的系数为0,求y的值.
试题解析:⑴【解析】
A-2B=2x2+3xy+2y-1–2(x2-xy+x- )
)
=5xy–2x+2y
当x=y=-2时,原式=20
⑵原式= (5y–2)x+2y
由题意得5y–2=0
所以y=
考点:1.整式的加减;2.多项式系数、次数

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的一元二次方程
的一元二次方程 的一个根是0,则
的一个根是0,则 的值是 .
的值是 .
 中,
中, ,
, .动点
.动点 分别在直线
分别在直线 上运动,且始终保持
上运动,且始终保持 .设
.设 ,
, ,则
,则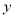 与
与 之间的函数关系用图象大致可表示为 ( )
之间的函数关系用图象大致可表示为 ( )

 的值为18,则代数式
的值为18,则代数式 的值等于 .
的值等于 .
 B.
B.
 D.
D.