题目内容
 已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB=
已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB=| 3 | 4 |
分析:作梯形的两条高,构造了一个矩形和两个直角三角形.根据角平分线的定义和平行线的性质得到等腰三角形ACD,即CD=AD=5.再根据锐角三角函数的概念得到AE:BE,结合勾股定理得到BE:AB=3:5,从而求得BE的长,再进一步计算出CF和EF的长.
解答: 解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示,
解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示,
∵AC平分∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AD=DC.∵AD=5,AB=DC,
∴AD=DC=AB=5.
过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∴∠AEB=90°.
在Rt△AEB中,
tanB=
=
.
设AE=3x,则BE=4x.
∵AB=5,
∴(3x)2+(4x)2=52.
∴x=1(负值舍去).
∴AE=3,BE=4.同理可得FC=4.
∵AE⊥BC,DF⊥BC,
∴AE∥DF.
∵AD∥BC,
∴四边形AEFD是平行四边形.
∴EF=AD=5.
∴BC=13.
 解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示,
解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示,∵AC平分∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AD=DC.∵AD=5,AB=DC,
∴AD=DC=AB=5.
过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∴∠AEB=90°.
在Rt△AEB中,
tanB=
| AE |
| BE |
| 3 |
| 4 |
设AE=3x,则BE=4x.
∵AB=5,
∴(3x)2+(4x)2=52.
∴x=1(负值舍去).
∴AE=3,BE=4.同理可得FC=4.
∵AE⊥BC,DF⊥BC,
∴AE∥DF.
∵AD∥BC,
∴四边形AEFD是平行四边形.
∴EF=AD=5.
∴BC=13.
点评:本题考查解直角三角形的知识,注意掌握作两高也是梯形中常见的辅助线之一.能够发现等腰三角形,运用锐角三角函数的知识得到边之间的关系,从而求得该梯形的下底.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 27、已知:如图,AD∥BC,ED∥BF,且AF=CE.
27、已知:如图,AD∥BC,ED∥BF,且AF=CE. 25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.
25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.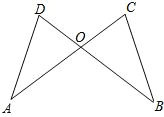 已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.
已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.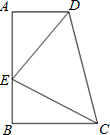 已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC. 根据题意填空:
根据题意填空: