题目内容
(1998•台州)如图,ABCD为正方形,E、F分别在BC、CD上,且△AEF为正三角形,四边形A′B′C′D′为△AEF的内接正方形,△A′E′F′为正方形A′B′C′D′的内接正三角形.(1)试猜想
 与
与 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;(2)求
 的值.
的值.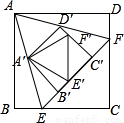
【答案】分析:(1)由于所有的正方形都相似,所有的等边三角形也都相似,而相似三角形面积的比等于相似比的平方,所以只需比较 与
与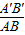 的大小.
的大小.
(2)由于正△AEF既是正方形ABCD的内接正三角形,同时四边形A′B′C′D′又为△AEF的内接正方形,所以将AE作为中间量,求出A′B′:AB的值.
解答:解:(1)相等.
∵正方形ABCD和等边三角形AEF都是轴对称图形,直线AC是它的公共对称轴,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,
又∵∠BAE+∠DAF+∠EAF=90°,∠EAF=60°,
∴∠BAE=15°,
∴AE= ,
,
同理,A′E′= ,
,
∴ =
= ,
,
∵所有的正方形都相似,所有的等边三角形也都相似,而相似三角形面积的比等于相似比的平方,
∴ =
= ,
, =
= ,
,
∴ =
= ;
;
(2)由(1)知△ABE≌△ADF,
∴BE=DF,
∴CE=CF,
设正方形ABCD的边长是a,等边三角形AEF边长为x,
∵CE2+CF2=x2,∴CE= x,
x,
∴BE=a- x,
x,
∵x2=(a- x )2+a2,
x )2+a2,
∴x2+2 ax-4a2=0,
ax-4a2=0,
舍去负根,得x=( -
- )a,
)a,
∴AE=(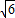 -
- )AB,
)AB,
设正方形A′B′C′D′的边长是y,由于△A′B′E≌△D′C′F,
∴B′E=C′F= (x-y),
(x-y),
在△A′B′E中,∠A′B′E=90°,∠B′A′E=30°,
∴B′E:A′B′= (x-y):y=tan30°=
(x-y):y=tan30°= :3,
:3,
∴y=(2 -3)x,
-3)x,
∴A′B′=(2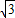 -3)AE,
-3)AE,
∴ =
=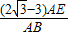 =
= =9
=9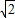 -5
-5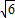 ,
,
∴ =(9
=(9 -5
-5 )2=312-180
)2=312-180 .
.
点评:本题主要考查了正方形与等边三角形的性质的运用.
 与
与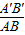 的大小.
的大小.(2)由于正△AEF既是正方形ABCD的内接正三角形,同时四边形A′B′C′D′又为△AEF的内接正方形,所以将AE作为中间量,求出A′B′:AB的值.
解答:解:(1)相等.
∵正方形ABCD和等边三角形AEF都是轴对称图形,直线AC是它的公共对称轴,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,
又∵∠BAE+∠DAF+∠EAF=90°,∠EAF=60°,
∴∠BAE=15°,
∴AE=
 ,
,同理,A′E′=
 ,
,∴
 =
= ,
,∵所有的正方形都相似,所有的等边三角形也都相似,而相似三角形面积的比等于相似比的平方,
∴
 =
= ,
, =
= ,
,∴
 =
= ;
;(2)由(1)知△ABE≌△ADF,
∴BE=DF,
∴CE=CF,
设正方形ABCD的边长是a,等边三角形AEF边长为x,
∵CE2+CF2=x2,∴CE=
 x,
x,∴BE=a-
 x,
x,∵x2=(a-
 x )2+a2,
x )2+a2,∴x2+2
 ax-4a2=0,
ax-4a2=0,舍去负根,得x=(
 -
- )a,
)a,∴AE=(
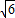 -
- )AB,
)AB,设正方形A′B′C′D′的边长是y,由于△A′B′E≌△D′C′F,
∴B′E=C′F=
 (x-y),
(x-y),在△A′B′E中,∠A′B′E=90°,∠B′A′E=30°,
∴B′E:A′B′=
 (x-y):y=tan30°=
(x-y):y=tan30°= :3,
:3,∴y=(2
 -3)x,
-3)x,∴A′B′=(2
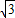 -3)AE,
-3)AE,∴
 =
=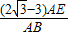 =
= =9
=9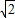 -5
-5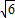 ,
,∴
 =(9
=(9 -5
-5 )2=312-180
)2=312-180 .
.点评:本题主要考查了正方形与等边三角形的性质的运用.

练习册系列答案
相关题目






