题目内容
 如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边交于点F.
如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边交于点F.
①若BE=1,EC=2,则sin∠EDC=________;
②若BE:EC=1:4,则BF:AF=________.
 4:5
4:5分析:①由四边形ABCD是矩形与折叠的性质,即可得DE=AD=BC=2,又由BE=1,EC=2,即可求得EC的值,然后由sin∠EDC=
 即可求得答案;
即可求得答案;②由同角的余角相等,即可求得∠BFE=∠DEC,然后由余弦三角函数的性质,即可得BF:EF的值,由折叠的性质,即可得BF:AF的值.
解答:①∵BE=1,EC=2,
∴BC=BE+EC=3
∵四边形ABCD是矩形,
∴AD=BC=3,∠A=∠B=∠C=90°,
根据折叠的性质可得:ED=AD=BC=3,
∵BE=1,
在Rt△DEC中,sin∠EDC=
 =
= ;
;②∵四边形ABCD是矩形,
∴AD=BC=3,∠A=∠B=∠C=90°,
根据折叠的性质可得:∠DEF=∠A=90°,AD=DE=BC,AF=EF,
∵BE:EC=1:4,
∴BE=x,EC=4x,
∴DE=5x,
∴∠BEF+∠BFE=90°,∠BEF+∠CED=90°,
∴∠BFE=∠CED,
∴cos∠EFB=cos∠CED=
 =
= =
= ,
,∴BF:AF=BF:EF=4:5.
故答案为:①
 ,②4:5.
,②4:5.点评:此题考查了折叠的性质,三角函数,矩形的性质以及直角三角形的性质等知识.此题综合性较强,难度较大,解题的关键是数形结合思想的应用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 23、如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
23、如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.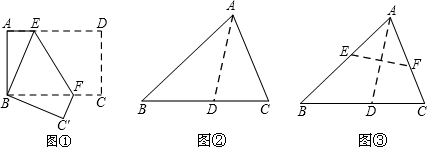
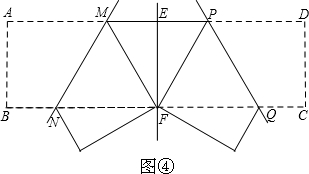
 (2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( )
(2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( ) 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
