题目内容
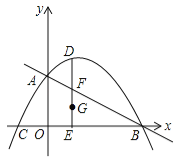
【题目】如图,抛物线![]() 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式,
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标.
【答案】(1)![]() ;(2)2或
;(2)2或![]() .
.
【解析】
试题分析:
(1)根据B,C两点在抛物线上,代入抛物线得到方程组,求出a,b的值即可;
(2)先求出直线AB的解析式为![]() ,设F点的坐标为(x,
,设F点的坐标为(x,![]() ),则D点的坐标为(x,
),则D点的坐标为(x,![]() ),根据G点与D点关于F点对称,所以G点的坐标为(x,
),根据G点与D点关于F点对称,所以G点的坐标为(x,![]() ),若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,分两种情况试题解析:①若⊙G与x轴相切则必须由DG=GE;②若⊙G与y轴相切则必须由DG=OE.
),若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,分两种情况试题解析:①若⊙G与x轴相切则必须由DG=GE;②若⊙G与y轴相切则必须由DG=OE.
试题解析:
解:(1)∵B,C两点在抛物线![]() 上,
上,
∴![]() ,解得:
,解得: .
.
∴所求的抛物线为:![]() ;
;
(2)抛物线![]() ,则点A的坐标为(0,2),
,则点A的坐标为(0,2),
设直线AB的解析式为![]() ,
,
∴![]() ,解得:
,解得: ,
,
∴直线AB的解析式为![]() ,
,
设F点的坐标为(x,![]() ),则D点的坐标为(x,
),则D点的坐标为(x,![]() ),
),
∵G点与D点关于F点对称,
∴G点的坐标为(x,![]() ),
),
若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,
①若⊙G与x轴相切则必须有DG=GE,
即:![]() =
=![]() ,
,
即:![]() ,
,
解得:![]() ,
,![]() (舍去);
(舍去);
②若⊙G与y轴相切则必须由DG=OE,
即![]() ,
,
解得:![]() ,
,![]() (舍去);
(舍去);
综上,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,G点的横坐标为2或![]() ;
;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目