题目内容
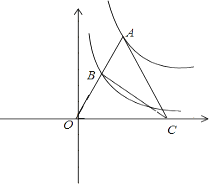
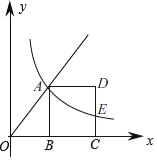
【题目】如图,点A是射线y=![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】A
【解析】
设点A的坐标为:(m,![]() m),得到正方形的边长,根据点A在双曲线上,得到k关于m的表达式,根据点A的横坐标和正方形的边长,得到点C,D,E的横坐标,代入反比例函数的解析式,得到点E的纵坐标,即EC的长度,结合正方形的边长,得到DE的长度,即可得到答案.
m),得到正方形的边长,根据点A在双曲线上,得到k关于m的表达式,根据点A的横坐标和正方形的边长,得到点C,D,E的横坐标,代入反比例函数的解析式,得到点E的纵坐标,即EC的长度,结合正方形的边长,得到DE的长度,即可得到答案.
解:设点A的坐标为:(m,![]() m),
m),
∵点A在双曲线y=![]() 上,
上,
∴k=![]() ,
,
即反比例函数的解析式为:y=![]() ,
,
AB=AD=CD=BC=![]() m,
m,
点C,D,E的横坐标为:m+![]() m=
m=![]() m,
m,
把x=![]() m代入反比例函数y=
m代入反比例函数y=![]() 得:
得:
y=![]() m,
m,
即EC=![]() m,DE=
m,DE=![]() m﹣
m﹣![]() m=
m=![]() m,
m,
![]() ,
,
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目