Question

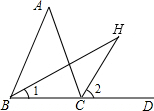已知如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC的平分线．
求证：∠A=2∠H．
证明：∵∠ACD是△ABC的一个外角，
∴∠ACD=∠ABC+∠A（________）
∠2是△BCH的一个外角，
∠2=∠1+∠H（________）
∵CH是外角∠ACD的平分线，BH是∠ABC的平分线
∴∠1=∠ABC，∠2=∠ACD（________）
∴∠A=∠ACD-∠ABC=2（∠2-∠1）（等式的性质）
而∠H=∠2-∠1（等式的性质）
∴∠A=2∠H（________）

Answer 1

三角形的一个外角等于和它不相邻的两个内角的和    三角形的一个外角等于和它不相邻的两个内角的和    角平分线的定义    等量代换
分析：此题主要注意思路：根据三角形的外角进行角的转换，再结合角平分线的概念进行等量代换．
解答：三角形的一个外角等于和它不相邻的两个外角的和；
三角形的一个外角等于和它不相邻的两个外角的和；
角平分线的定义；
等量代换．
点评：要熟悉几何定理的语言表达，能够准确叙述定理的内容．