题目内容
已知平行四边形ABCD与平行四边形A′B′C′D′相似，AB=3，对应边A′B′=4，若平行四边形ABCD的面积为18，则平行四边形A′B′C′D′的面积为
- A.
- B.
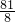
- C.24
- D.32
D
分析：利用相似多边形对应边之比、周长之比等于相似比，而面积之比等于相似比的平方可得．
解答：平行四边形ABCD与平行四边形A′B′C′D′相似，
AB=3，对应边A′B′=4，
因而这两个平行四边形的相似比是3：4，
因而面积的比是9：16，
因而平行四边形A′B′C′D′的面积是32．
点评：本题考查相似多边形的性质．
分析：利用相似多边形对应边之比、周长之比等于相似比，而面积之比等于相似比的平方可得．
解答：平行四边形ABCD与平行四边形A′B′C′D′相似，
AB=3，对应边A′B′=4，
因而这两个平行四边形的相似比是3：4，
因而面积的比是9：16，
因而平行四边形A′B′C′D′的面积是32．
点评：本题考查相似多边形的性质．
练习册系列答案
快捷英语周周练系列答案
相关题目
20、如图，已知平行四边形ABCD．
，连接DF，并延长DF交AB的延长线于点E，连接CE．
49、如图，已知平行四边形ABCD，AE平分∠DAB交DC于E，BF平分∠ABC交DC于F，DC=6cm，AD=2cm，求DE、EF、FC的长．
已知平行四边形ABCD中，对角线BD平分∠ABC，求证：四边形ABCD是菱形．