题目内容
 如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为
如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为
- A.(-4,0)
- B.(-2,0)
- C.(-4,0)或(-2,0)
- D.(-3,0)
D
分析:此题根据切线的性质以及勾股定理,把要求PQ的最小值转化为求AP的最小值,再根据垂线段最短的性质进行分析求解.
解答: 解:连接AQ,AP.
解:连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
则根据垂线段最短,则作AP⊥x轴于P,即为所求作的点P;
此时P点的坐标是(-3,0).
故选D.
点评:此题应先将问题进行转化,再根据垂线段最短的性质进行分析.
分析:此题根据切线的性质以及勾股定理,把要求PQ的最小值转化为求AP的最小值,再根据垂线段最短的性质进行分析求解.
解答:
 解:连接AQ,AP.
解:连接AQ,AP.根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
则根据垂线段最短,则作AP⊥x轴于P,即为所求作的点P;
此时P点的坐标是(-3,0).
故选D.
点评:此题应先将问题进行转化,再根据垂线段最短的性质进行分析.

练习册系列答案
相关题目
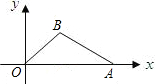 sin∠BOA=
sin∠BOA= 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.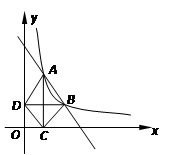

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.