题目内容
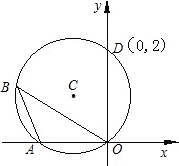 如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(________);C(________).
如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(________);C(________).
- ,0 -
,0 - ,1
,1
分析:连AD,由于∠AOD=90°,则AD过点C,由∠ADC=∠OBA=30°,设OA=x,则AD=2x,通过勾股定理求出OA,可得到A点坐标;而C点为AD的中点,由A,D两点坐标可直接写出C点坐标.
解答: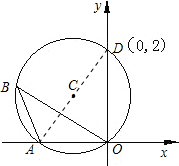 解:连AD,如图,
解:连AD,如图,
∵∠AOD=90°,
∴AD为直径,即AD过点C,
又有∠ADO=∠OBA=30°,设OA=x,则AD=2x,
所以(2x)2-x2=22,解得x= ,即OA=
,即OA= .
.
∴A点坐标为(- ,0),
,0),
又∵C点为AD的中点,
∴C点坐标为(- ,1).
,1).
故答案为(- ,0),(-
,0),(- ,1).
,1).
点评:本题考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.同时考查了90度的圆周角所对的弦为直径以及点的坐标的表示.
 ,0 -
,0 - ,1
,1分析:连AD,由于∠AOD=90°,则AD过点C,由∠ADC=∠OBA=30°,设OA=x,则AD=2x,通过勾股定理求出OA,可得到A点坐标;而C点为AD的中点,由A,D两点坐标可直接写出C点坐标.
解答:
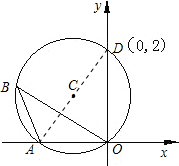 解:连AD,如图,
解:连AD,如图,∵∠AOD=90°,
∴AD为直径,即AD过点C,
又有∠ADO=∠OBA=30°,设OA=x,则AD=2x,
所以(2x)2-x2=22,解得x=
 ,即OA=
,即OA= .
.∴A点坐标为(-
 ,0),
,0),又∵C点为AD的中点,
∴C点坐标为(-
 ,1).
,1).故答案为(-
 ,0),(-
,0),(- ,1).
,1).点评:本题考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.同时考查了90度的圆周角所对的弦为直径以及点的坐标的表示.

练习册系列答案
相关题目
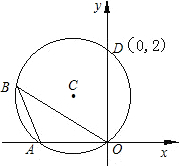 如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(
如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(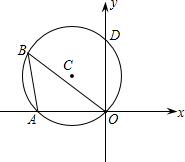 如图,⊙C通过原点,并与坐标轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则点C的坐标为
如图,⊙C通过原点,并与坐标轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则点C的坐标为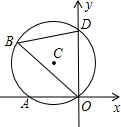 如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为
如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为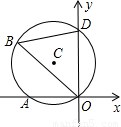 如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为 .
如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为 .