题目内容
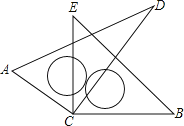
【题目】如图,四边形![]() 是矩形纸片且
是矩形纸片且![]() ,对折矩形纸片
,对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,展平后再过点
,展平后再过点![]() 折叠矩形纸片,使点
折叠矩形纸片,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 与
与![]() 相交于点
相交于点![]() ,再次展开,连接
,再次展开,连接![]() ,
,![]() .
.
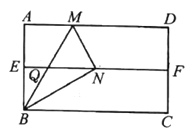
(1)连接![]() ,求证:
,求证:![]() 是等边三角形;
是等边三角形;
(2)求![]() ,
,![]() 的长;
的长;
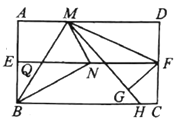
(3)如图,连接![]() 将
将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,延长
处,延长![]() 交
交![]() 边于点
边于点![]() ,已知
,已知![]() ,求
,求![]() 的长?
的长?
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由折叠知![]() ,据此得∠ENB=30°,∠ABN=60°,结合AB=BN即可得证;
,据此得∠ENB=30°,∠ABN=60°,结合AB=BN即可得证;
(2)由(1)得∠ABN=60°,由AB折叠到BN知∠ABM=30°,结合AB=6得![]() ,证EQ为△ABM的中位线得
,证EQ为△ABM的中位线得![]() ,再求出EN=
,再求出EN=![]() ,根据QN=EN-EQ可得答案;
,根据QN=EN-EQ可得答案;
(3)连接FH,MK⊥BC,证Rt△FGH≌Rt△FCH得GH=CH=1,设MD=x,知MG=x,MH=x+1,KH=MD-CH=x-1,在Rt△MKH中,根据MK2+KH2=MH2可求出x的值,继而得出答案.
解:(1)![]() 与
与![]() 重合后,折痕为
重合后,折痕为![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 为等边三角形.
为等边三角形.
(2)由(1)得![]() ,
,
![]() 折叠到
折叠到![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() 为
为![]() 的中点且
的中点且![]() ,
,
![]() 为
为![]() 的中位线.
的中位线.
![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() .
.
(3)连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
![]() 折叠到
折叠到![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
![]() .设
.设![]() ,
,
![]() ,
,
![]() .
.
![]()
在![]() 中,
中,![]() ,
,![]() ,解得
,解得![]() ,
,![]() .
.

练习册系列答案
相关题目