题目内容
若关于x的一元二次方程2x2-2x+3m-1=0的两个实数根x1,x2,且x1•x2>x1+x2-4,则实数m的取值范围是
- A.m>

- B.m≤

- C.m<

- D.
 <m≤
<m≤
D
分析:关于x的一元二次方程2x2-2x+3m-1=0的两个实数根x1,x2,根据根与系数的关系得到x1+x2= =1,x1•x2=
=1,x1•x2= =
=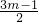 ,然后将其代入x1•x2>x1+x2-4可得关于m的不等式,解不等式即可求出m的取值范围.同时一元二次方程2x2-2x+3m-1=0的有两个实数根,有△=b2-4ac≥0,也得到关于m的不等式,也可以得到一个m的取值范围.把两个范围结合起来即可求出m的取值范围.
,然后将其代入x1•x2>x1+x2-4可得关于m的不等式,解不等式即可求出m的取值范围.同时一元二次方程2x2-2x+3m-1=0的有两个实数根,有△=b2-4ac≥0,也得到关于m的不等式,也可以得到一个m的取值范围.把两个范围结合起来即可求出m的取值范围.
解答:依题意得x1+x2= =1,x1•x2=
=1,x1•x2= =
=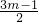 ,
,
而x1•x2>x1+x2-4,
∴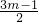 >-3,
>-3,
得m> ;
;
又一元二次方程2x2-2x+3m-1=0的有两个实数根,
∴△=b2-4ac≥0,
即4-4×2×(3m-1)≥0,
解可得m≤ .
.
∴ <m≤
<m≤ .
.
故选D.
点评:本题考查一元二次方程ax2+bx+c=0的根与系数关系即韦达定理,两根之和是 ,两根之积是
,两根之积是 .
.
分析:关于x的一元二次方程2x2-2x+3m-1=0的两个实数根x1,x2,根据根与系数的关系得到x1+x2=
 =1,x1•x2=
=1,x1•x2= =
=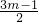 ,然后将其代入x1•x2>x1+x2-4可得关于m的不等式,解不等式即可求出m的取值范围.同时一元二次方程2x2-2x+3m-1=0的有两个实数根,有△=b2-4ac≥0,也得到关于m的不等式,也可以得到一个m的取值范围.把两个范围结合起来即可求出m的取值范围.
,然后将其代入x1•x2>x1+x2-4可得关于m的不等式,解不等式即可求出m的取值范围.同时一元二次方程2x2-2x+3m-1=0的有两个实数根,有△=b2-4ac≥0,也得到关于m的不等式,也可以得到一个m的取值范围.把两个范围结合起来即可求出m的取值范围.解答:依题意得x1+x2=
 =1,x1•x2=
=1,x1•x2= =
=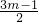 ,
,而x1•x2>x1+x2-4,
∴
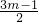 >-3,
>-3,得m>
 ;
;又一元二次方程2x2-2x+3m-1=0的有两个实数根,
∴△=b2-4ac≥0,
即4-4×2×(3m-1)≥0,
解可得m≤
 .
.∴
 <m≤
<m≤ .
.故选D.
点评:本题考查一元二次方程ax2+bx+c=0的根与系数关系即韦达定理,两根之和是
 ,两根之积是
,两根之积是 .
. 
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目