题目内容
等腰三角形底边上的高是8cm，周长是32cm，且腰长与底边长的比为5：6，则这个三角形的面积是________cm2．
48
分析：根据已知列方程从而求得底边与腰的长，再根据面积公式求解．
解答：设腰长为x，则底边长为32-2x，由题意知x=
（32-2x），
解得x=10，
则底边长为32-20=12，
故这个三角形的面积为
×8×12=48（cm2）．
故填48．
点评：本题考查等腰三角形的性质、三角形的周长与面积公式的运用；求得底边的长是正确解答本题的关键．
分析：根据已知列方程从而求得底边与腰的长，再根据面积公式求解．
解答：设腰长为x，则底边长为32-2x，由题意知x=
（32-2x），解得x=10，
则底边长为32-20=12，
故这个三角形的面积为
×8×12=48（cm2）．故填48．
点评：本题考查等腰三角形的性质、三角形的周长与面积公式的运用；求得底边的长是正确解答本题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
等腰三角形底边上的高等于底边的一半，则这个等腰三角形的顶角度数是（ ）
| A、30° | B、45° | C、90° | D、120° |
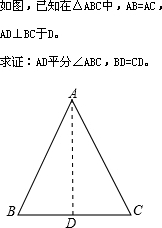小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时，画出图形，写出“已知”、“求证”（如图）．