Question

【题目】在平面直角坐标系xOy中，已知抛物线y＝﹣x2+2mx﹣m2+m．

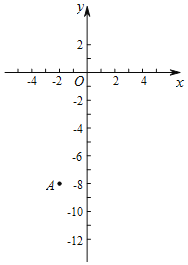
（1）求抛物线的对称轴（用含m的式子表示）；

（2）如果该抛物线的顶点在直线y＝2x﹣4上，求m的值.

（3）点A的坐标为（﹣2，﹣8），点A关于点（0，﹣9）的对称点为B点．

①写出点B坐标.

②若该抛物线与线段AB有公共点，结合函数图象，直接写出m的取值范围．

Answer 1

【答案】（1）对称轴方程为：x＝m；（2）m＝4；（3）①B（2，﹣10）；②当﹣4≤m≤﹣1或1≤m≤6时，抛物线与线段AB有公共点．

【解析】

（1）根据二次函数y=ax2+bx+c(a≠0)的对称轴方程为x=解答即可；（2）把二次函数解析式化成顶点式，可得顶点坐标，代入y＝2x﹣4求出m值即可；（3）①设B（x，y），根据中点坐标公式即可求出B点坐标；②分别把A、B两点坐标代入y＝﹣x2+2mx﹣m2+m，求出m的值，根据图象即可得m的取值范围.

（1）抛物线y＝﹣x2+2mx﹣m2+m对称轴方程为：x＝﹣＝m，

（2）∵y＝﹣x2+2mx﹣m2+m＝﹣（x﹣m）2+m，

∴顶点坐标为（m，m），

∵抛物线顶点在直线y＝2x﹣4上，

∴m＝2m﹣4，

∴m＝4；

（3）①设B（x，y），

∵点A的坐标为（﹣2，﹣8），点A关于点（0，﹣9）的对称点为B点，

∴＝0，＝﹣9，

∴B（2，﹣10）；

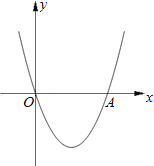
②如图所示：把A（﹣2，﹣8）代入y＝﹣x2+2mx﹣m2+m得，﹣8＝﹣4﹣4m﹣m2+m，

解得m＝1或m＝﹣4，

把B（2，﹣10）代入y＝mx2﹣4mx+2m﹣1得，﹣10＝﹣4+4m﹣m2+m，

解得m＝6或m＝﹣1，

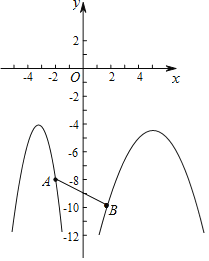
∴当﹣4≤m≤﹣1或1≤m≤6时，抛物线与线段AB有公共点．