题目内容
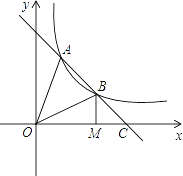
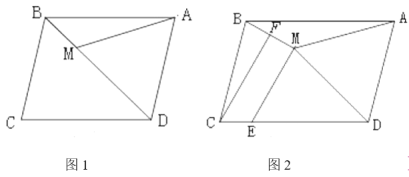
【题目】如图,在平面直角坐角系中,点![]() 是原点,点
是原点,点![]() 、
、![]() 在坐标轴上,连接
在坐标轴上,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 是线段
是线段![]() 的垂直平分线上一点.
的垂直平分线上一点.
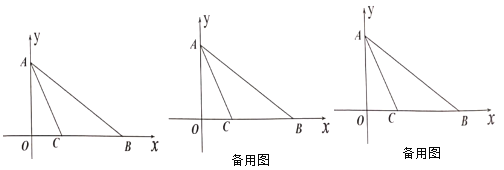
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发以每秒2个单位长度的速度向终点
出发以每秒2个单位长度的速度向终点![]() 运动(点
运动(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 、
、![]() ,若点
,若点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,过点![]() 作
作![]() 垂直
垂直![]() 轴,交
轴,交![]() 于
于![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)S=
;(2)S=![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)依据三角形内角和定理、线段中垂线的性质、等腰三角形等边对等角,得到![]() ,再依据含30度的直角三角形的性质得到
,再依据含30度的直角三角形的性质得到![]() ,最终建立BC和OC的关系,即可求出OC的长和C的坐标;
,最终建立BC和OC的关系,即可求出OC的长和C的坐标;
![]() 作
作![]() 于N,由题意得
于N,由题意得![]() ,则
,则![]() ,由直角三角形的性质得出
,由直角三角形的性质得出![]() ,由三角形面积公式即可得出答案;
,由三角形面积公式即可得出答案;
(3)先求证![]() ,再分点
,再分点![]() 与点
与点![]() 重合、点
重合、点![]() 有
有![]() 上两种情况讨论,对于第2种情况,先证明
上两种情况讨论,对于第2种情况,先证明![]() ,再依据30度的直角三角形的性质,得到
,再依据30度的直角三角形的性质,得到![]() ,再证明
,再证明![]() ,依据等腰三角形三线合一的性质得到
,依据等腰三角形三线合一的性质得到![]() ,最后得到
,最后得到![]() ,即可写出点
,即可写出点![]() 的坐标.
的坐标.
解:(1)![]() ,
,![]()
![]()
![]() 点
点![]() 是线段
是线段![]() 的垂直平分线上一点
的垂直平分线上一点
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
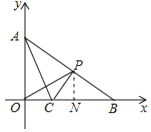
过点![]() 作
作![]() 于N,
于N,
![]()
![]()
![]()
![]() ;
;
(3)![]() 轴,
轴,
![]()
![]()
![]()
![]()
又![]()
![]()
①当点![]() 与点
与点![]() 重合时,
重合时,![]()
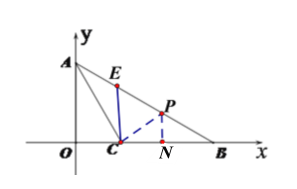
②当点![]() 有
有![]() 上时,连接
上时,连接![]() ,
,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
综上所述:![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】八(2)班分成甲、乙两组进行一分钟投篮测试,并规定得6分及以上为合格,得9分及以上为优秀,现两组学生的一次测试成绩统计如下表:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组人数(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组人数(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上表数据,把下面的统计表补充完整,并写出求甲组平均分的过程;
统计量 | 平均分 | 方差 | 众数 | 中位数 | 合格率 | 优秀率 |
甲组 |
| 2.56 |
| 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 |
| 86.7% | 13.3% |
(2)如果从投篮的稳定性角度进行评价,你认为哪组成绩更好?并说明理由;
(3)小聪认为甲组成绩好于乙组,请你说出支持小聪观点的理由;