题目内容
抛物线y=x2+2x-3与x轴的交点的个数有
- A.O个
- B.1个
- C.2个
- D.3个
C
分析：利用△判定二次函数图象与x轴的交点的情况即可解答．
解答：△=22-4×（-3）＞0，抛物线y=x2+2x-3与x轴有两个交点．
故选C．
点评：主要考查了二次函数的性质与一元二次方程之间的关系．
分析：利用△判定二次函数图象与x轴的交点的情况即可解答．
解答：△=22-4×（-3）＞0，抛物线y=x2+2x-3与x轴有两个交点．
故选C．
点评：主要考查了二次函数的性质与一元二次方程之间的关系．
练习册系列答案
名校课堂系列答案
相关题目
抛物线y=x2+2x-2的图象上最低点的坐标是（ ）
| A、（2，-2） | B、（1，-2） | C、（1，-3） | D、（-1，-3） |
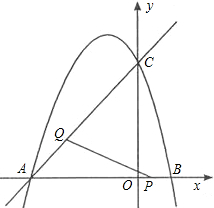秒，请求出△APQ的面积S与t的函数关系式，并求出当t为何值时，△APQ的面积最大，最大面积是多少？