题目内容
（2012•香坊区三模）在△ABC中，∠ACB=2∠BAC，点E在AC上，连接BE，且AE=BE，CD平分∠ACB交AB于点D
，连接DE．
（1）（如图1），求证：BD=ED；
（2）设线段CD、BE相交于点P，将∠CAB沿直线AC翻折得到∠CAB′（如图2），射线AB′交BE延长线于点Q，连接CQ，若DE：BC=2：3，S四边形ADPQ=
，求∠ACQ的正切值．
，连接DE．（1）（如图1），求证：BD=ED；
（2）设线段CD、BE相交于点P，将∠CAB沿直线AC翻折得到∠CAB′（如图2），射线AB′交BE延长线于点Q，连接CQ，若DE：BC=2：3，S四边形ADPQ=
| 39 |
| 4 |
| 7 |
分析：（1）根据条件CD平分∠ACB可以得出∠ACB=2∠ACD=2∠BCD从而得出∠ACD=∠BCD=∠A=∠ABE，最后通过证明△ADE≌△CDB就可以得出结论；
（2）由DE：BC=2：3，设DE=4k，BC=6k，可以得出AE=BE=BC=6k，从而可以得出∠DBE=∠EBA，就有△BDE∽△BEA，由相似三角形的性质就可以表示出AB=9k，AD=CD=5k，再由∠DBP=∠BCD，∠BDP=∠CDB，可以得出△BDP∽△CDB，从而求出BP=
k，PD=
k．过点D作DF⊥BE于F，根据勾股定理可以求出DF的值，可以表示出sin∠FBD=
=
，cos∠QAC=
=
．进而求得S△PBD的值，再由条件可以证明△PBD∽△QBA，求出S△PBD：S△QBA的比值，由其条件建立方程求出k的值，过Q作QH⊥AC于H，在Rt△AHQ中，HQ=AQ•sin∠QAC=
，AH=AQ•cos∠QAC=
，通过△ADC∽△AEB就可以得出CH的值，从而就可以求出
∠ACQ的正切值．
（2）由DE：BC=2：3，设DE=4k，BC=6k，可以得出AE=BE=BC=6k，从而可以得出∠DBE=∠EBA，就有△BDE∽△BEA，由相似三角形的性质就可以表示出AB=9k，AD=CD=5k，再由∠DBP=∠BCD，∠BDP=∠CDB，可以得出△BDP∽△CDB，从而求出BP=
| 24 |
| 5 |
| 16 |
| 5 |
| DF |
| BD |
| ||
| 4 |
| BF |
| BD |
| 3 |
| 4 |
9
| ||
| 5 |
| 27 |
| 5 |
∠ACQ的正切值．
解答：（1）证明：∵CD平分∠ACB，
∴∠ACB=2∠ACD=2∠BCD．
∵AE=BE，
∴∠A=∠ABE．
∵∠ACB=2∠A，
∴∠ACD=∠BCD=∠A=∠ABE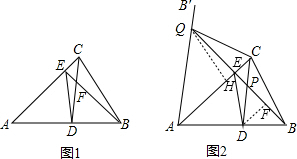
∴AD=CD．
∵∠BEC=∠A+∠ABE=2∠A=2∠ACD，
∴∠BEC=∠ACB，
∴BC=BE，BC=AE，
∵在△ADE和△CDB中，
，
∴△ADE≌△CDB（SAS），
∴DE=DB，即BD=ED．
（2）解：∵DE：BC=2：3，设DE=4k，BC=6k，
∴AE=BE=BC=6k．
∵BD=ED，
∴∠DEB=∠DBE，
∴∠EAB=∠DEB．
∵∠DBE=∠EBA，
∴△BDE∽△BEA，
∴
=
，
∴
=
，
∴AB=9k．
∴AD=CD=5k．
∵∠DBP=∠BCD，∠BDP=∠CDB，
∴△BDP∽△CDB，
∴
=
=
，
∴
=
，
∴BP=
k，PD=
k．
过点D作DF⊥BE于F，
∵BD=ED，DF⊥BE，
∴BF=EF=
BE=3k．
∴在Rt△BFD中，DF=
=
k，
∴sin∠FBD=
=
，cos∠QAC=
=
．
∵∠QAC=∠BAC=∠FBD，
∴sin∠QAC=
=
，cos∠QAC=
=
，
∴S△PBD=
BP•DF=
×
k×
k=
k2．
∵∠QAC=∠BAC，
∴∠QAC=∠ACB，
∴PD∥AQ，
∴△PBD∽△QBA，
∴S△PBD：S△QBA=BD2：BA2=（4k）2：（9k）2=16：81，
=
=
．
∴S四边形ADPQ=S△QBA-S△PBD=
∴S△PBD：S四边形ADPQ=16：65，AQ=
k，
∴
k2：
=16：65，
∴k=1，k=-1（舍去）
∴AQ=
．
过Q作QH⊥AC于H，
∴在Rt△AHQ中，HQ=AQ•sin∠QAC=
，AH=AQ•cos∠QAC=
，．
∵∠ACD=∠ABE，∠CAD=∠BAE，∴△ADC∽△AEB，
∴
=
，
∴
=
，
∴AC=
k=
，
∴CH=AC-AH=
，
∴在Rt△CHQ中，tan∠ACQ=
=
=
．
∴∠ACB=2∠ACD=2∠BCD．
∵AE=BE，
∴∠A=∠ABE．
∵∠ACB=2∠A，
∴∠ACD=∠BCD=∠A=∠ABE
∴AD=CD．
∵∠BEC=∠A+∠ABE=2∠A=2∠ACD，
∴∠BEC=∠ACB，
∴BC=BE，BC=AE，
∵在△ADE和△CDB中，
|
∴△ADE≌△CDB（SAS），
∴DE=DB，即BD=ED．
（2）解：∵DE：BC=2：3，设DE=4k，BC=6k，
∴AE=BE=BC=6k．
∵BD=ED，
∴∠DEB=∠DBE，
∴∠EAB=∠DEB．
∵∠DBE=∠EBA，
∴△BDE∽△BEA，
∴
| BE |
| AB |
| BD |
| BE |
∴
| 6k |
| AB |
| 4k |
| 6k |
∴AB=9k．
∴AD=CD=5k．
∵∠DBP=∠BCD，∠BDP=∠CDB，
∴△BDP∽△CDB，
∴
| BP |
| BC |
| DB |
| DC |
| PD |
| BD |
∴
| BP |
| 6k |
| 4k |
| 5k |
∴BP=
| 24 |
| 5 |
| 16 |
| 5 |
过点D作DF⊥BE于F，
∵BD=ED，DF⊥BE，
∴BF=EF=
| 1 |
| 2 |
∴在Rt△BFD中，DF=
| BD2-BF2 |
| 7 |
∴sin∠FBD=
| DF |
| BD |
| ||
| 4 |
| BF |
| BD |
| 3 |
| 4 |
∵∠QAC=∠BAC=∠FBD，
∴sin∠QAC=
| DF |
| BD |
| ||
| 4 |
| BF |
| BD |
| 3 |
| 4 |
∴S△PBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
| 7 |
12
| ||
| 5 |
∵∠QAC=∠BAC，
∴∠QAC=∠ACB，
∴PD∥AQ，
∴△PBD∽△QBA，
∴S△PBD：S△QBA=BD2：BA2=（4k）2：（9k）2=16：81，
| PD |
| QA |
| BD |
| BA |
| 4k |
| 9k |
∴S四边形ADPQ=S△QBA-S△PBD=
| 39 |
| 4 |
| 7 |
∴S△PBD：S四边形ADPQ=16：65，AQ=
| 36 |
| 5 |
∴
12
| ||
| 5 |
39
| ||
| 4 |
∴k=1，k=-1（舍去）
∴AQ=
| 36 |
| 5 |
过Q作QH⊥AC于H，
∴在Rt△AHQ中，HQ=AQ•sin∠QAC=
9
| ||
| 5 |
| 27 |
| 5 |
∵∠ACD=∠ABE，∠CAD=∠BAE，∴△ADC∽△AEB，
∴
| AC |
| AB |
| CD |
| BE |
∴
| AC |
| 9k |
| 5k |
| 6k |
∴AC=
| 5 |
| 12 |
| 5 |
| 12 |
∴CH=AC-AH=
| 21 |
| 10 |
∴在Rt△CHQ中，tan∠ACQ=
| QH |
| CH |
| ||||
|
6
| ||
| 7 |
点评：本题是一道综合性极强几何综合试题，考查了全等三角形的判定及性质的运用，相似三角形的判定及性质的运用，勾股定理放入性质的运用，三角函数值的运用，利用参数法求解的运用，解答时灵活运用相似三角形的性质求解是解答本题的关键，正确作出辅助线是解答本题的难点．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
（2012•香坊区三模）图中几何体从左边看得到的图形是（ ）
（2012•香坊区三模）如图，在△ABC中，∠C=90°，AC=4，BC=3，AB边上有一点D，且AD=AC，过点D作DE⊥AB交BC于点E，则△BDE的周长是（ ）