题目内容
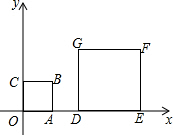如图，正方形OABC和正方形DEFG是位似图形（其中点O，A，B，C的对应点分别是点D，E，F，G），点B的坐标为（1，1），点F的坐标为（4，2），则这两个正方形的位似中心的坐标是________．
（-2，0）或（
，
）
分析：根据两个位似图形的主要特征是：每对位似对应点与位似中心共线；不经过位似中心的对应线段平行．则位似中心就是两对对应点的延长线的交点，求出直线BF所在解析式即可．
解答：
解：两个位似图形时，位似中心就是BF与x轴的交点，
设直线BF解析式为y=kx+b，将F（4，2），B（1，1）代入，得
，
解得：
，
即y=
x+，
令y=0得x=-2，
∴O′坐标是（-2，0）；
同理O″坐标是（，）．
故答案为：（-2，0），（，）．
点评：本题主要考查位似图形的性质，根据每对位似对应点与位似中心共线得出是解题关键．
，）分析：根据两个位似图形的主要特征是：每对位似对应点与位似中心共线；不经过位似中心的对应线段平行．则位似中心就是两对对应点的延长线的交点，求出直线BF所在解析式即可．
解答：
解：两个位似图形时，位似中心就是BF与x轴的交点，设直线BF解析式为y=kx+b，将F（4，2），B（1，1）代入，得
，解得：
，即y=x+，令y=0得x=-2，
∴O′坐标是（-2，0）；
同理O″坐标是（
，）．故答案为：（-2，0），（
，）．点评：本题主要考查位似图形的性质，根据每对位似对应点与位似中心共线得出是解题关键．
练习册系列答案
备战中考寒假系列答案
相关题目
的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S．（提示：考虑点P在点B的左侧或右侧两种情况）
如图，正方形OABC、ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B、E在函数
如图，正方形OABC和正方形ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数y=
如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为
象上，点P（m，n）是函数