题目内容
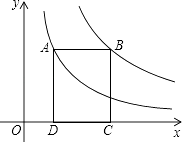
【题目】在平面上，Rt△ABC与直径为CE的半圆O，如图1摆放，∠B=90°，BC=m，AC=2CE=n，半圆O交BC边于点D，将半圆O绕点C按逆时针方向旋转，点D随半圆O旋转，且∠ECD=∠ACB，旋转角记为α（0°≤α≤180°）． 
（1）①当α=0°时，连接DE，则∠CDE=°，CD=；②当α=180°时， 
= ．
（2）试判断：旋转过程中 的大小有无变化？请仅就图2的情形给出证明．
（3）若m=4，n=5，当α=∠ACB时，线段BD= ．
（4）若m=4 
，n=6，当半圆O旋转至与△ABC的边相切时，线段BD= ．
【答案】
（1）90；
m；
（2）如图3中，
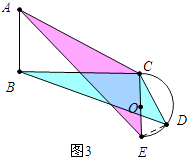
∵∠ACB=∠DCE，
∴∠ACE=∠BCD，
∵ 
= 
= ，
∴△ACE∽△BCD，
∴ 
= = ；
（3）
（4）2 
或 
【解析】（1）解：①如图1中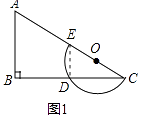 
当α=0时，连接DE，则∠CDE=90°，
∵∠CDE=∠B=90°，
∴DE∥AB，
∴ 
= 
= ，
∵BC=m，
∴CD= m，
所以答案是90°， m，
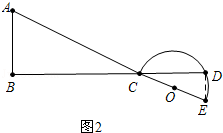
②如图2中，当α=180°时，BD=BC+CD= 
m，AE=AC+CE= n，
∴ = ．
所以答案是 ；
⑶如图4中，当α=∠ACB时，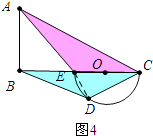
在Rt△ABC中，∵AC=5，BC=4，
∴AB= 
=3，
在Rt△ABE中．∵AB=3，BE=BC﹣CE=1.5，
∴AE= 
= 
= 
，
由（2）可知△ACE∽△BCD，
∴ = ，
∴ 
= 
，
∴BD= ，
所以答案是 ；
⑷∵m=4 
，n=6，
∴CE=3，CD=2 ，AB= 
=2，
①如图5中，当α=90°时，半圆与AC相切，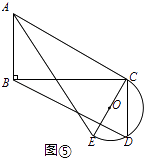
在Rt△DBC中，BD= 
=2 ．
②如图6中，当α=90°+∠ACB时，半圆与BC相切，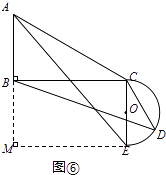
作EM⊥AB于M，
∵∠M=∠CBM=∠BCE=90°，
∴四边形BCEM是矩形，
∴BM=CE=3，ME=4 ，
∴AM=5，AE= 
= 
，
由（2）可知 
= 
，
∴BD= ．
所以答案是2 或 ．
