题目内容
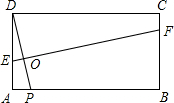
在矩形ABCD中,对角线AC,BD相交于点O,若AC=6cm,∠BOC=120°,则∠ACB=________,AB=________cm,BC=________cm.
30° 3 3
分析:根据矩形的对角线相等且互相平分可得OB=OC,再根据等腰三角形的两底角相等列式求出∠ACB,根据直角三角形30°角所对的直角边等于斜边的一半可得AB= AC,利用勾股定理列式求解即可得到BC的长度.
AC,利用勾股定理列式求解即可得到BC的长度.
解答: 解:在矩形ABCD中,OB=OC,
解:在矩形ABCD中,OB=OC,
∵∠BOC=120°,
∴∠ACB= (180°-∠BOC)=
(180°-∠BOC)= ×(180°-120°)=30°,
×(180°-120°)=30°,
∴AB= AC=
AC= ×6=3cm,
×6=3cm,
在Rt△ABC中,BC= =
= =3
=3 cm.
cm.
故答案为:30°;3;3 .
.
点评:本题考查了矩形的对角线相等且互相平分的性质,等腰三角形的性质,勾股定理和直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质是解题的关键,作出图形更形象直观.

分析:根据矩形的对角线相等且互相平分可得OB=OC,再根据等腰三角形的两底角相等列式求出∠ACB,根据直角三角形30°角所对的直角边等于斜边的一半可得AB=
 AC,利用勾股定理列式求解即可得到BC的长度.
AC,利用勾股定理列式求解即可得到BC的长度.解答:
 解:在矩形ABCD中,OB=OC,
解:在矩形ABCD中,OB=OC,∵∠BOC=120°,
∴∠ACB=
 (180°-∠BOC)=
(180°-∠BOC)= ×(180°-120°)=30°,
×(180°-120°)=30°,∴AB=
 AC=
AC= ×6=3cm,
×6=3cm,在Rt△ABC中,BC=
 =
= =3
=3 cm.
cm.故答案为:30°;3;3
 .
.点评:本题考查了矩形的对角线相等且互相平分的性质,等腰三角形的性质,勾股定理和直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 ,或许对你有所帮助哦!
,或许对你有所帮助哦!

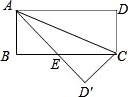 如图,在矩形ABCD中,AB=5,BC=12,将矩形ABCD沿对角线对折,然后放在桌面上,折叠后所成的图形覆盖桌面的面积是
如图,在矩形ABCD中,AB=5,BC=12,将矩形ABCD沿对角线对折,然后放在桌面上,折叠后所成的图形覆盖桌面的面积是 在矩形ABCD中,△ABD沿对角线BD对折,A与A′重合,AD=8,AB=6,A′D与BC相交于O.
在矩形ABCD中,△ABD沿对角线BD对折,A与A′重合,AD=8,AB=6,A′D与BC相交于O.