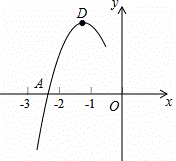题目内容
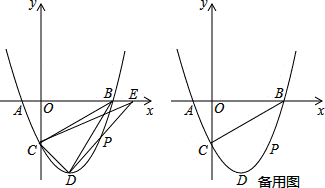
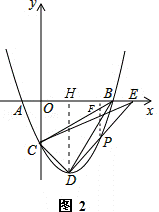
如图,在平面直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD、BD、DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.
解:(1)∵y=x2﹣2x﹣3=(x﹣3)(x+2),
∴由题意得,A(﹣1,0),B(3,0),C(0,﹣3),D(1,﹣4).
在Rt△OBC中,
∵OC=OB=3,
∴△OBC为等腰直角三角形,
∴∠OBC=45°.
(2)如图1,过点D作DH⊥x轴于H,此时S四边形OCDB=S梯形OCDH+S△HBD,
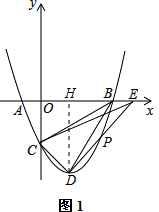
∵OH=1,OC=3,HD=4,HB=2,
∴S梯形OCDH= •(OC+HD)•OH=
•(OC+HD)•OH=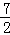 ,S△HBD=
,S△HBD= •HD•HB=4,
•HD•HB=4,
∴S四边形OCDB=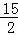 .
.
∴S△OCE=S四边形OCDB=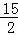 =
= ,
,
∴OE=5,
∴E(5,0).
设lDE:y=kx+b,
∵D(1,﹣4),E(5,0),
∴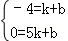 ,
,
解得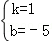 ,
,
∴lDE:y=x﹣5.
∵DE交抛物线于P,设P(x,y),
∴x2﹣2x﹣3=x﹣5,
解得 x=2 或x=1(D点,舍去),
∴xP=2,代入lDE:y=x﹣5,
∴P(2,﹣3).
(3)如图2,
设lBC:y=kx+b,
∵B(3,0),C(0,﹣3),
∴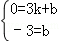 ,
,
解得 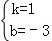 ,
,
∴lBC:y=x﹣3.
∵F在BC上,
∴yF=xF﹣3,
∵P在抛物线上,
∴yP=xP2﹣2xP﹣3,
∴线段PF长度=yF﹣yP=xF﹣3﹣(xP2﹣2xP﹣3),
∵xP=xF,
∴线段PF长度=﹣xP2+3xP=﹣(xP﹣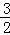 )2+
)2+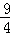 ,(1<xP≤3),
,(1<xP≤3),
∴当xP=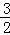 时,线段PF长度最大为
时,线段PF长度最大为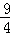 .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案已知 是二元一次方程组
是二元一次方程组 的解,则m﹣n的值是( )
的解,则m﹣n的值是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 ,则其侧面展开图的圆心角为(
,则其侧面展开图的圆心角为(  )
) 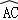 ,
,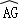 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.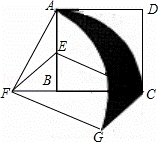
 的解,则代数式x2﹣4y2的值为
的解,则代数式x2﹣4y2的值为