Question

某天然气供应站根据实际情况，每天从零点开始至凌晨4点，只打开进气阀，在以后的16小时（4：00-20：00），同时打开进气阀和供气阀，20：00-24：00只打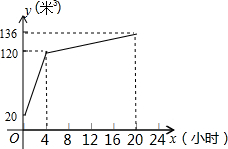开供气阀．已知气站每小时的进气量和供气量是一定的，如图反映了气站某天的储气量y （米³）与x（小时）之间的关系． 
（1）①0：00-4：00之间气站每小时增加的储气量为

25

米³，
②4：00-20：00之间气站每小时增加的储气量为

1

米³；
（2）求20：00-24：00时，y与x的函数关系式，并画出函数图象．

Answer 1

分析：（1）根据函数图象分别求出0：00-4：00之间4：00-20：00之间增加的储气量，再除以时间即可求出气站每小时增加的储气量；
（2）先求出气站每小时供气量，再根据20：00-24：00只打开供气阀，即可求出24时的储气量，得点（20，136）和点（24，40）满足y与x的函数关系式，再用待定系数法求出函数解析式，即可画出图象．

解答：解：（1）①由图象可知：
∵0：00-4：00之间气站储气量从20米³增加到120米³，
∴0：00-4：00之间气站每小时增加的储气量为：（120-20）÷4=25（米³）；
②同理可得：
4：00-20：00之间气站每小时增加的储气量为：

136-120

20-4

=1（米³）；

（2）∵气站每小时进气25米³，4：00-20：00之间气站每小时增加的储气量为1米³，
∴气站每小时供气量为 25-1=24（米³），
∴24时储气量为136-24×4=40（米³），
∴点（20，136）和点（24，40）满足y与x的函数关系式，
设所求函数关系式为y=kx+b，
则有

136=20k+b 40=24k+b

，
解得

k=-24 b=616

，
∴y与x的函数关系式为y=-24x+616，
图象如图所示：
．

点评：此题考查了一次函数的应用，用到的知识点是函数的图象、待定系数法求函数解析式，关键是根据函数图象获得有关信息，求出一次函数的解析式．