题目内容
正方形ABCD的边长为1,AB、AD上各有一点P、Q,如果 的周长为2,求
的周长为2,求 的度数。
的度数。

【答案】
45°.
【解析】
试题分析:首先从△APQ的周长入手求出PQ=DQ+BP,然后将△CDQ逆时针旋转90°,使得CD、CB重合,然后利用全等来解.
试题解析:如图所示,
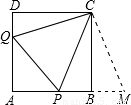
△APQ的周长为2,即AP+AQ+PQ=2①,
正方形ABCD的边长是1,即AQ+QD=1,AP+PB=1,
∴AP+AQ+QD+PB=2②,
①-②得,PQ-QD-PB=0,
∴PQ=PB+QD.
延长AB至M,使BM=DQ.连接CM,△CBM≌△CDQ(SAS),
∴∠BCM=∠DCQ,CM=CQ,
∵∠DCQ+∠QCB=90°,
∴∠BCM+∠QCB=90°,即∠QCM=90°,
PM=PB+BM=PB+DQ=PQ.
在△CPQ与△CPM中,
CP=CP,PQ=PM,CQ=CM,
∴△CPQ≌△CPM(SSS),
∴∠PCQ=∠PCM=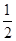 ∠QCM=45°.
∠QCM=45°.
考点:(1)正方形的性质;(2)全等三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 附加题
附加题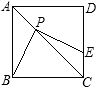 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3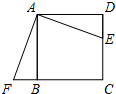 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=