Question

如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线DC，P点为优弧上一动点（不与A．C重合）．
（1）求∠APC与∠ACD的度数；
（2）当点P移动到CB弧的中点时，求证：四边形OBPC是菱形．
（3）P点移动到什么位置时，△APC与△ABC全等，请说明理由．

Answer 1

解：（1）连接AC，如图所示：

∵AB=4，∴OA=OB=OC=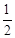AB=2。
又∵AC=2，∴AC=OA=OC。∴△ACO为等边三角形。
∴∠AOC=∠ACO=∠OAC=60°，
∴∠APC=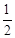∠AOC=30°。
又DC与圆O相切于点C，∴OC⊥DC。∴∠DCO=90°。
∴∠ACD=∠DCO﹣∠ACO=90°﹣60°=30°。
（2）连接PB，OP，
∵AB为直径，∠AOC=60°，∴∠COB=120°。
当点P移动到弧CB的中点时，∠COP=∠POB=60°。
∴△COP和△BOP都为等边三角形。∴AC=CP=OA=OP。
∴四边形AOPC为菱形。
（3）当点P与B重合时，△ABC与△APC重合，显然△ABC≌△APC。
当点P继续运动到CP经过圆心时，△ABC≌△CPA，理由为：
∵CP与AB都为圆O的直径，∴∠CAP=∠ACB=90°。
在Rt△ABC与Rt△CPA中，AB=CP，AC=AC
∴Rt△ABC≌Rt△CPA（HL）。
综上所述，当点P与B重合时和点P运动到CP经过圆心时，△ABC≌△CPA。

解析