题目内容
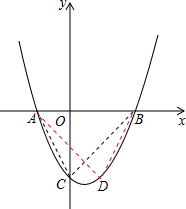
 如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;
如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;
(2)若与x轴的两个交点为A、B,与y轴交于点C.在该抛物线上找一点D,使得△ABC与△ABD全等,求出D点的坐标.
 解:(1)由题意,得
解:(1)由题意,得 ,
,解得,
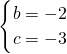 ,
,所以,该抛物线的解析式为:y=x2-2x-3;
(2)∵抛物线y=x2-2x-3的对称轴为:x=-
 =1,
=1,∴根据轴对称的性质,点C关于x=1的对称点D即为所求,
此时,AC=BD,BC=AD,
在△ABC和△BAD中,
∵
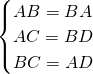 ,
,∴△ABC≌△BAD(SSS).
在y=x2-2x-3中,令x=0,得y=-3,
则C(0,-3),
∴D(2,-3).
分析:(1)把点(1,-4)和(-2,5)分别代入该二次函数解析式,列出关于b、c的方程组
 ,通过解该方程组即可求得它们的值;
,通过解该方程组即可求得它们的值;(2)首先由抛物线y=ax2+bx+c的对称轴是x=-
 ,即可求得此抛物线的对称轴,根据轴对称的性质,点C关于x=1的对称点D即为所求,利用SSS即可判定△ABC≌△BAD,又由抛物线的与y轴交于点C,即可求得点C的坐标,由对称性可求得D点的坐标.
,即可求得此抛物线的对称轴,根据轴对称的性质,点C关于x=1的对称点D即为所求,利用SSS即可判定△ABC≌△BAD,又由抛物线的与y轴交于点C,即可求得点C的坐标,由对称性可求得D点的坐标.点评:此题考查了待定系数法求二次函数的解析式、二次函数的性质、全等三角形的判定与二次函数的对称性.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
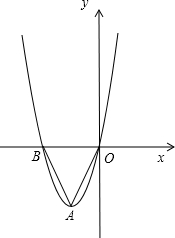 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B. 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.