题目内容
?ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;④AO=DO,使得?ABCD是菱形的条件有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:四边形ABCD是平行四边形,要是其成为菱形,加上一组邻边相等或对角线垂直均可.
解答:∵四边形ABCD是平行四边形,
①若AC⊥BD,则可得其为菱形,故①选项正确,
②中一组邻边相等,也可得到一菱形,所以②成立,
③若AC平分∠BAD;则可证得:AB=BC,所以③成立,
④若AO=DO则AC=BD,所以四边形ABCD为矩形,所以④不成立,
则能使?ABCD是菱形的有①或③或②.
故选:C.
点评:此题考查了菱形的判定,即对角线互相垂直的平行四边形是菱形,有一组邻边相等的平行四边形是菱形,需熟练掌握菱形的两个基本判定.
分析:四边形ABCD是平行四边形,要是其成为菱形,加上一组邻边相等或对角线垂直均可.
解答:∵四边形ABCD是平行四边形,
①若AC⊥BD,则可得其为菱形,故①选项正确,
②中一组邻边相等,也可得到一菱形,所以②成立,

③若AC平分∠BAD;则可证得:AB=BC,所以③成立,
④若AO=DO则AC=BD,所以四边形ABCD为矩形,所以④不成立,
则能使?ABCD是菱形的有①或③或②.
故选:C.
点评:此题考查了菱形的判定,即对角线互相垂直的平行四边形是菱形,有一组邻边相等的平行四边形是菱形,需熟练掌握菱形的两个基本判定.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
平行四边形ABCD的对角线AC和BD相交点O,与△OBC面积相等的三角形(不包括自身)的个数是
| A. 1 | B.2 | C.3 | D.4 |
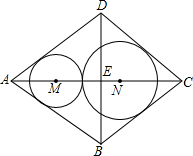 形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.
形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由. 如图,已知矩形ABCD的对角线AC,BD的相交点O,E、F、G、H分别是OA、OB、OC、OD的中点.
如图,已知矩形ABCD的对角线AC,BD的相交点O,E、F、G、H分别是OA、OB、OC、OD的中点.
 如图,已知矩形ABCD的对角线AC,BD的相交点O,E、F、G、H分别是OA、OB、OC、OD的中点.
如图,已知矩形ABCD的对角线AC,BD的相交点O,E、F、G、H分别是OA、OB、OC、OD的中点.