题目内容
如图，点F是正方形ABCD外一点，且△ABF为等边三角形，则∠CFD的度数为30°
30°
．分析：根据正方形的性质与等边三角形的性质求出∠DAF，AD=AF=AB，然后根据等腰三角形两底角相等求出∠AFD，同理可求∠BFC，再根据∠AFB=60°列式进行计算即可得解．
解答：解：∵四边形ABCD是正方形，△ABF为等边三角形，
∴∠DAF=90°+60°=150°，AD=AF=AB，
∴∠AFD=
（180°-∠DAF）=
（180°-150°）=15°，
同理可得：∠BFC=15°，
∴∠CFD=60°-15°×2=30°．
故答案为：30°．
∴∠DAF=90°+60°=150°，AD=AF=AB，
∴∠AFD=
| 1 |
| 2 |
| 1 |
| 2 |
同理可得：∠BFC=15°，
∴∠CFD=60°-15°×2=30°．
故答案为：30°．
点评：本题考查了正方形的性质，等边三角形的性质，以及等腰三角形两底角相等的性质，熟练掌握正方形与等边三角形的性质是解题的关键．
练习册系列答案
相关题目
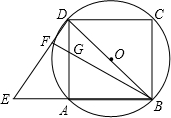如图，点E是正方形ABCD边BA延长线上一点（AE＜AD），连接DE．与正方形ABCD的外接圆相交于点F，BF与AD相交于点G．
（2013•包头）如图，点E是正方形ABCD内的一点，连接AE、BE、CE，将△ABE绕点B顺时针旋转90°到△CBE′的位置．若AE=1，BE=2，CE=3，则∠BE′C=
如图，点E是正方形ABCD边BC的中点，H是BC延长线上的一点，EG⊥AE于点E，交边CD于G，
（2013•青铜峡市模拟）如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB、EA．
如图，点M是正方形ABCD的边CD的中点，正方形ABCD的边长为4cm，点P按A-B-C-M-D的顺序在正方形的边上以每秒1cm的速度作匀速运动，设点P的运动时间为x（秒），△APM的面积为y（cm2）