Question

【题目】阅读与思考；

婆罗摩笈多是一位印度数学家与天文学家，书写了两部关于数学与天文的书籍，他的一些数学成就在世界数学史上有较高的地位，他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的，他还提出了著名的婆罗摩笈多定理，该定理的内容及证明如下：

已知：如图，四边形ABCD内接与圆O对角线AC⊥BD于点M，ME⊥BC于点E，延长EM交CD于F，求证：MF=DF

证明∵AC⊥BD，ME⊥BC

∴∠CBD=∠CME

∵∠CBD=∠CAD，∠CME=∠AMF

∴∠CAD=∠AMF

∴AF=MF

∵∠AMD=90°，同时∠MAD+∠MDA=90°

∴∠FMD=∠FDM

∴MF=DF，即F是AD中点．

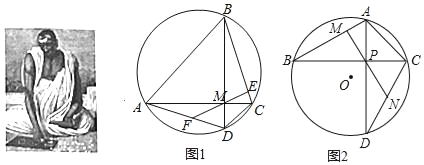
（1）请你阅读婆罗摩笈多定理的证明过程，完成婆罗摩笈多逆定理的证明：

已知：如图1，四边形ABCD内接与圆O，对角线AC⊥BD于点M，F是AD中点，连接FM并延长交BC于点E，求证：ME⊥BC

（2）已知如图2，△ABC内接于圆O，∠B=30°∠ACB=45°，AB=2，点D在圆O上，∠BCD=60°，连接AD 交BC于点P，作ON⊥CD于点N，延长NP交AB于点M，求证PM⊥BA并求PN的长．

Answer 1

【答案】（1）证明见解析;（2）证明见解析, PN=1．

【解析】试题分析：（1）由于AC⊥BD，所以∠AMD=90°，∠FAM+∠FDM=90°，由于F是AD的中点，所以AF=MF=DF，从而可证明∠EMC+∠MCB=90°．

（2）由圆周角定理得出∠D=∠B=30°，由三角形内角和定理求出∠DAC=45°，得出△APC是等腰直角三角形，∴PA=PC，∠CPD=90°，由（1）的证明过程可知：PM⊥BA，再由含30°的直角三角形的性质即可求出AP=1，CD=2，最后利用直角三角形斜边上的中线等于斜边的一半即可求出PN的长度．

试题解析：（1）∵AC⊥BD，

∴∠AMD=90°，

∵F是AD的中点，

∴AF=MF=DF，

∴∠FAM=∠FMA，

∠FMD=∠FDM，

∵∠FDM=∠MCB，∠FMA=∠EMC，

∠FAM+∠FDM=90°

∴∠EMC+∠MCB=90°，

∴ME⊥BC；

（2）∵∠ACB=45°，∠BCD=60°，

∴∠ACD=45°+60°=105°，

又∵∠D=∠B=30°，

∴∠DAC=180°﹣∠ACD﹣∠D=45°，

∴∠APC=180°﹣45°﹣45°=90°，△APC是等腰直角三角形，

∴PA=PC，∠APC=90°，

∴AD⊥BC，

∵ON⊥CD，

∴由垂径定理可知：N是CD的中点，

∴由（1）的证明过程可知：PM⊥BA

∵AB=2，∠B=30°，

∴AP=1，

∴PC=1，

∵∠D=30°，

∴CD=2PC=2，

∵N是CD的中点，∠CPD=90°，

∴PN=CD=1．