题目内容
 如图,用12米长的木材做一个中间有一条横档的日字形窗户.设AB=x米
如图,用12米长的木材做一个中间有一条横档的日字形窗户.设AB=x米
(1)用含x的代数式表示线段AC的长;
(2)若使透进窗户的光线达到6平方米,则窗户的长和宽各为多少?
(3)透进窗户的光线能达到9平方米吗?如果能,请求出这个窗户的长和宽;如果不能,请说明理由.
解:(1)设AB=x米,
∵AC+BD+3AB=12,
2AC=12-3x,
∴AC=BD= (m),
(m),
(2)∵窗户面积=AB•AC=6,
∴由(1)得出:x( )=6,
)=6,
整理得出:x2-4x+4=0,
解得:x1=x2=2,
则 =3,
=3,
即窗户的长和宽各为:3m,2m.
(3)由(2)得出:x( )=9,
)=9,
整理得出:x2-4x+6=0,
△=b2-4ac=16-4×6=-8<0,
故此方程没有实数根,则透进窗户的光线不能达到9平方米.
分析:(1)根据矩形周长求法得出AC的关系式即可;
(2)利用矩形面积公式求出x( )=6,进而得出x的值即可;
)=6,进而得出x的值即可;
(2)利用一元二次方程根的判别式求出△,即可判定方程根的情况.
点评:此题主要考查了一元二次方程的应用以及根的判别式等知识,根据图形表示出AC的长是解题关键.
∵AC+BD+3AB=12,
2AC=12-3x,
∴AC=BD=
 (m),
(m),(2)∵窗户面积=AB•AC=6,
∴由(1)得出:x(
 )=6,
)=6,整理得出:x2-4x+4=0,
解得:x1=x2=2,
则
 =3,
=3,即窗户的长和宽各为:3m,2m.
(3)由(2)得出:x(
 )=9,
)=9,整理得出:x2-4x+6=0,
△=b2-4ac=16-4×6=-8<0,
故此方程没有实数根,则透进窗户的光线不能达到9平方米.
分析:(1)根据矩形周长求法得出AC的关系式即可;
(2)利用矩形面积公式求出x(
 )=6,进而得出x的值即可;
)=6,进而得出x的值即可;(2)利用一元二次方程根的判别式求出△,即可判定方程根的情况.
点评:此题主要考查了一元二次方程的应用以及根的判别式等知识,根据图形表示出AC的长是解题关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
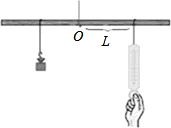 如图,取一根长1米长的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:
如图,取一根长1米长的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:| L/cm | 1 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| F/牛顿 | 125 | 24.5 | 16.5 | 12.3 | 9.8 | 8.2 | 7 | █ | 5.4 |
(1)当L=
(2)被墨水涂黑了的数据你认为大概是
(3)你能求出F与L的函数关系式吗?
(4)请你在直角坐标系中画出此函数的图象.
