题目内容
如图，梯形OABC是正六边形的一部分，画出它关于x轴对称的其余部分，如果AB的长为2，求出各顶点的坐标．分析：首先找出A、B点关于x轴的对称点，再顺次连接，然后根据正六边形的性质可得AO=AB=BC=2，∠AOC=60°，再根据三角函数值计算出OM、NC的长，进而得到各点坐标．
解答：
解：如图所示：∠AOC=60°，
过A作AM⊥OC，过B作BN⊥⊥OC，
∵梯形OABC是正六边形的一部分，
∴∠AOC=60°，AO=AB=BC=2，
∴OM=AO×cos60°=1，AM=AO×sin60°=
，
CN=CB×cos60°=1，BN=
，
∴A（1，
），B（3，
），C（4，0），D（3，-
），
E（1，-
）．
解：如图所示：∠AOC=60°，过A作AM⊥OC，过B作BN⊥⊥OC，
∵梯形OABC是正六边形的一部分，
∴∠AOC=60°，AO=AB=BC=2，
∴OM=AO×cos60°=1，AM=AO×sin60°=
| 3 |
CN=CB×cos60°=1，BN=
| 3 |
∴A（1，
| 3 |
| 3 |
| 3 |
E（1，-
| 3 |
点评：此题主要考查了做轴对称变换，以及正多边形的性质，关键是掌握正六边形每个内角都是120°，每条边都相等．
练习册系列答案
相关题目
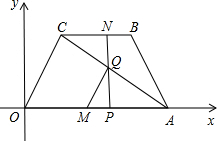度向终点C运动（M到达点A后停止，点N继续运动到C点停止），过点N作NP⊥OA于P点，连接AC交NP于Q，连接MQ，如动点N运动时间为t秒．
度向终点C运动（M到达点A后停止，点N继续运动到C点停止），过点N作NP⊥OA于P点，连接AC交NP于Q，连接MQ，如动点N运动时间为t秒．
如图，梯形OABC是正六边形的一部分，画出它关于x轴对称的其余部分，如果AB的长为2，求出各顶点的坐标．