题目内容
点A(-2,3)在反比例函数 的图象上,当1≤x≤6时,y的取值范围为________.
的图象上,当1≤x≤6时,y的取值范围为________.
-6≤y≤-1
分析:首先利用待定系数法求出反比例函数k的值,再根据反比例函数的性质:当k<0时,y随x的增大而增大,求出x=1时的y的值,再算出x=-6时的y值,即可得到答案.
解答:∵点A(-2,3)在反比例函数 的图象上,
的图象上,
∴k=xy=-2×3=-6,
∵k<0,
∴y随x的增大而增大,
∴当x=1时,y=-6,当x=6时,y=-1,
∴y的取值范围为-6≤y≤-1.
故答案为:-6≤y≤-1.
点评:此题主要考查了反比例函数的图象的性质,关键是掌握待定系数法求反比例函数解析式,以及反比例函数的性质.
分析:首先利用待定系数法求出反比例函数k的值,再根据反比例函数的性质:当k<0时,y随x的增大而增大,求出x=1时的y的值,再算出x=-6时的y值,即可得到答案.
解答:∵点A(-2,3)在反比例函数
 的图象上,
的图象上,∴k=xy=-2×3=-6,
∵k<0,
∴y随x的增大而增大,
∴当x=1时,y=-6,当x=6时,y=-1,
∴y的取值范围为-6≤y≤-1.
故答案为:-6≤y≤-1.
点评:此题主要考查了反比例函数的图象的性质,关键是掌握待定系数法求反比例函数解析式,以及反比例函数的性质.

练习册系列答案
相关题目
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.

⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
⑵如图3,⊙ 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).
⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙
 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
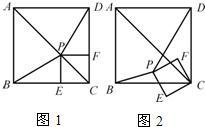 25、如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
25、如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.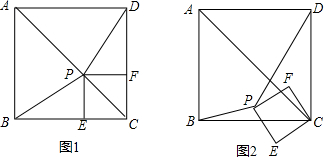
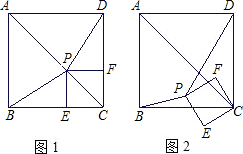 的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.