题目内容
如图1.在四边形ABCD中.AB=AD,∠B+∠D=180゜,E、F分别是边BC、CD上的点,且∠BAD=2∠EAF.
(1)求证:EF=BE+DF;
(2)在(1)问中,若将△AEF绕点A逆时针旋转,当点E、F分别运动到BC、CD延长线上时,如图2所示,
试探究EF、BE、DF之间的数量关系.

(1)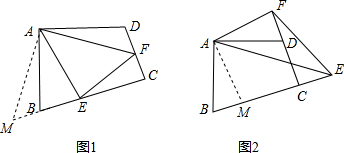 证明:延长CB至M,使BM=DF,连接AM,
证明:延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
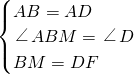
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
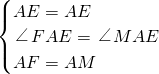 ,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
(2)解:发生变化,EF、BE、DF之间的关系是EF=BE-DF,
理由是:在CB上截取BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中,
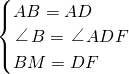
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD+DAF=∠BAM+∠MAD=2∠EAF,
∴∠EAM=∠EAF,
在△FAE和△MAE中,
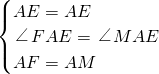 ,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE-BM=BE-DF,
即EF=BE-DF.
分析:(1)延长CB至M,使BM=DF,连接AM,证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
(2)在CB上截取BM=DF,连接AM,证△ABM≌△ADF,推出AF=AM,∠DAF=∠BAM,求出∠EAM=∠EAF,证△FAE≌△MAE,推出EF=EM即可.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是能正确作辅助线,证明过程类似.
 证明:延长CB至M,使BM=DF,连接AM,
证明:延长CB至M,使BM=DF,连接AM,∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
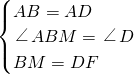
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
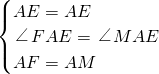 ,
,∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
(2)解:发生变化,EF、BE、DF之间的关系是EF=BE-DF,
理由是:在CB上截取BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中,
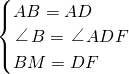
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD+DAF=∠BAM+∠MAD=2∠EAF,
∴∠EAM=∠EAF,
在△FAE和△MAE中,
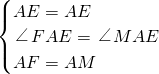 ,
,∴△FAE≌△MAE(SAS),
∴EF=EM=BE-BM=BE-DF,
即EF=BE-DF.
分析:(1)延长CB至M,使BM=DF,连接AM,证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
(2)在CB上截取BM=DF,连接AM,证△ABM≌△ADF,推出AF=AM,∠DAF=∠BAM,求出∠EAM=∠EAF,证△FAE≌△MAE,推出EF=EM即可.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是能正确作辅助线,证明过程类似.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目