题目内容
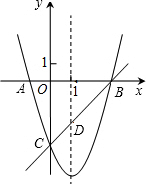 如图,已知抛物线y=x2+bx+c与x轴相交于A,B两点(A点在B点的左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
如图,已知抛物线y=x2+bx+c与x轴相交于A,B两点(A点在B点的左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的解析式;
(2)在抛物线上是否存在一点E,使得2S△ABE=S△ABC?若存在,求出点E的坐标;若不存在,请说明理由.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:计算题
分析:(1)把C点坐标代入得到c=-3,再根据抛物线对称轴方程求出b,从而得到抛物线解析式;
(2)先确定A、B、C点的坐标,再计算出S△ABC=6,则S△ABE=3,设E(x,x2-2x-3),利用三角形面积公式得到
•4•|x2-2x-3|=3,然后分别解两个一元二次方程即可得到E点坐标.
(2)先确定A、B、C点的坐标,再计算出S△ABC=6,则S△ABE=3,设E(x,x2-2x-3),利用三角形面积公式得到
| 1 |
| 2 |
解答:解:(1)根据题意得
,解得
所以抛物线解析式为y=x2-2x-3;
(2)存在.
当x=0时,y=x2-2x-3=-3,则C(0,-3),
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则点A(-1,0),B(3,0),
所以S△ABC=
×3×4=6,
而2S△ABE=S△ABC,
所以S△ABE=3,
设E(x,x2-2x-3),
所以
•4•|x2-2x-3|=3,
即2x2-4x-9=0或2x2-4x-3=0,
解2x2-4x-9=0得x1=
,x2=
解2x2-4x-3=0得x1=
,x2=
,
所以满足条件的E点坐标为(
,
),(
,
),(
,-
),(
,-
).
|
|
所以抛物线解析式为y=x2-2x-3;
(2)存在.
当x=0时,y=x2-2x-3=-3,则C(0,-3),
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则点A(-1,0),B(3,0),
所以S△ABC=
| 1 |
| 2 |
而2S△ABE=S△ABC,
所以S△ABE=3,
设E(x,x2-2x-3),
所以
| 1 |
| 2 |
即2x2-4x-9=0或2x2-4x-3=0,
解2x2-4x-9=0得x1=
2+
| ||
| 2 |
2-
| ||
| 2 |
解2x2-4x-3=0得x1=
2+
| ||
| 2 |
2-
| ||
| 2 |
所以满足条件的E点坐标为(
2+
| ||
| 2 |
| 3 |
| 2 |
2-
| ||
| 2 |
| 3 |
| 2 |
2+
| ||
| 2 |
| 3 |
| 2 |
2-
| ||
| 2 |
| 3 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
 如图,AO⊥BC,DO⊥OE.求证:∠AOD=∠COE,∠BOD=∠AOE.
如图,AO⊥BC,DO⊥OE.求证:∠AOD=∠COE,∠BOD=∠AOE.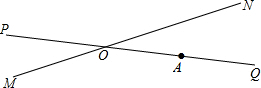 铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=300m,如果火车行驶时,周围250m以内都会受到噪音的影响,那么火车在铁路MN沿ON方向行驶时,居民楼是否会受到噪音的影响?请说明理由.如果火车行驶的速度是72km/h,居民楼受噪音影响的时间约为多少秒?(提示:过点A作MN的垂线段AC)
铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=300m,如果火车行驶时,周围250m以内都会受到噪音的影响,那么火车在铁路MN沿ON方向行驶时,居民楼是否会受到噪音的影响?请说明理由.如果火车行驶的速度是72km/h,居民楼受噪音影响的时间约为多少秒?(提示:过点A作MN的垂线段AC)